题目内容
17.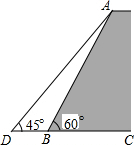 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 过A点作AE⊥CD于E,在Rt△ABE中,根据∠ABE=60°,AB=30m,求出AE的长度,然后再Rt△ADE中求出DE的长度,继而可求得BD的长度.
解答 解:过A点作AE⊥CD于E.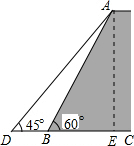
在Rt△ABE中,
∵∠ABE=60°.
∴AE=AB•sin60°=30×$\frac{\sqrt{3}}{2}$=15$\sqrt{3}$(米),
BE=AB•cos60°=30×$\frac{1}{2}$=15(米),
在Rt△ADE中,
∵∠ADB=45°,
∴DE=AE=15$\sqrt{3}$(米),
∴DB=DE-BE=15$\sqrt{3}$-15≈11.0(米).
故此时应将坝底向外拓宽大约11.0米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据题目所给的坡角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
相关题目
8.一组数据-1,2,3,-1,0的中位数和众数分别是( )
| A. | 2,-1 | B. | 0,-1 | C. | 1.5,0 | D. | D-1,0 |
5.直角坐标系中,P点在第四象限,则P点的坐标可能是( )
| A. | (6,-4) | B. | (5,2) | C. | (-3,-6) | D. | (-3,4) |
12.已知点M(-1,m)和点N(-2,n)是反比例函数y=$\frac{2}{x}$图象上的两点,则m与n的大小关系是( )
| A. | m<n | B. | m=n | C. | m>n | D. | 以上都不对 |
 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=52°,则∠2=104°.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=52°,则∠2=104°. 如图,若AE是△ABC的中线,BC=4,则BE=2.
如图,若AE是△ABC的中线,BC=4,则BE=2.