题目内容
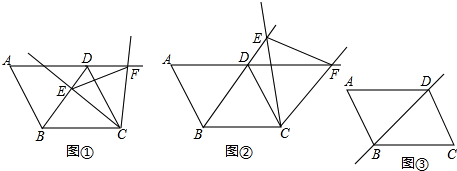
12. 如图,点E是平行四边形ABCD边AD上的一点,点G是CD的中点,连接EG并延长,交BC延长线于F,连接CE、DF.求证:四边形CEDF是平行四边形.
如图,点E是平行四边形ABCD边AD上的一点,点G是CD的中点,连接EG并延长,交BC延长线于F,连接CE、DF.求证:四边形CEDF是平行四边形.
分析 先根据ASA证明△CFG≌△DEG,得出对应边相等,再根据对角线互相平分的四边形是平行四边形即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴BC∥AD,∴BF∥AD,
∴∠FCG=∠EDG,
∵点G是CD的中点,
∴CG=DG,
在△CFG和△DEG中,$\left\{\begin{array}{l}{∠FCG=∠EDG}&{\;}\\{CG=DG}&{\;}\\{∠CGF=∠DGE}&{\;}\end{array}\right.$,
∴△CFG≌△DEG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形(对角线互相平分的四边形是平行四边形).
点评 本题考查了平行四边形的判定与性质;熟练掌握平行四边形的判定方法,通过证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
3.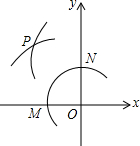 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )| A. | 6a-2b=1 | B. | 6a+2b=1 | C. | 6a-b=1 | D. | 6a+b=1 |
 如图,∠1与∠2,∠3与∠4,分别是什么关系?分别是哪两条直线被哪一条直线所截形成的?
如图,∠1与∠2,∠3与∠4,分别是什么关系?分别是哪两条直线被哪一条直线所截形成的?