题目内容
18.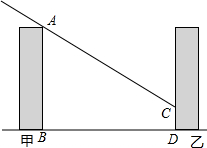 有一朝向为正南方向的楼,该楼的一楼是高5米的小区超市,超市以上是居民区,在该楼的前面20米处要盖一栋高16米的甲楼,当冬季正午的阳光与水平线的夹角为32°时.
有一朝向为正南方向的楼,该楼的一楼是高5米的小区超市,超市以上是居民区,在该楼的前面20米处要盖一栋高16米的甲楼,当冬季正午的阳光与水平线的夹角为32°时.(1)超市以上的居民区住房采光是否受影响?为什么?(sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
(2)若使阳光能照到D处,两楼应相距多少米?
分析 (1)利用三角函数算出阳光可能照到居民楼的什么高度,和5米进行比较即可;
(2)若阳光能照到D处,在Rt△ABD中根据新楼的高度和32°的正切值即可求出两楼应相距多少米.
解答 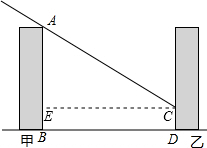 解:(1)超市以上的居民区住房采光不受影响.理由如下:
解:(1)超市以上的居民区住房采光不受影响.理由如下:
如图,作CE∥BD交AB于E.
设CD=x米,则AE=(16-x)米,
在Rt△AEC中,∵∠AEC=90°,
∴tan32°=$\frac{AE}{CE}$,即$\frac{16-x}{20}$≈0.62,
解得x≈3.6,
∵3.6<5,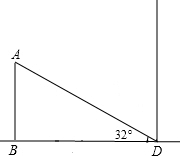 ∴超市以上的居民区住房采光不受影响.
∴超市以上的居民区住房采光不受影响.
(2)如图:在Rt△ABD中,∵∠ABD=90°,
∴tan32°=$\frac{AB}{BD}$,
∴BD≈16÷0.62≈25.81(米).
故若使阳光能照到D处,两楼应相距约25.81米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
8.一组数据-1,2,3,-1,0的中位数和众数分别是( )
| A. | 2,-1 | B. | 0,-1 | C. | 1.5,0 | D. | D-1,0 |
3.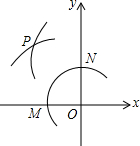 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )| A. | 6a-2b=1 | B. | 6a+2b=1 | C. | 6a-b=1 | D. | 6a+b=1 |
10.如图,某电视台的娱乐节目《周末大放送》有这样的翻奖牌游戏,数字的背面写有祝福语或奖金数,游戏规则是:每翻动正面一个数字,看看反面对应的内容,就可知是得奖还是得到温馨祝福.
正面
反面
计算:
(1)“翻到奖金1000元”的概率;
(2)“翻到奖金”的概率;
(3)“翻不到奖金”的概率.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 祝你 开心 | 万事 如意 | 奖金 1000元 |
| 身体 健康 | 心想 事成 | 奖金 500元 |
| 奖金 100元 | 生 活 愉快 | 谢谢 参与 |
计算:
(1)“翻到奖金1000元”的概率;
(2)“翻到奖金”的概率;
(3)“翻不到奖金”的概率.
 如图,若AE是△ABC的中线,BC=4,则BE=2.
如图,若AE是△ABC的中线,BC=4,则BE=2. 如图,∠l=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.
如图,∠l=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.