Question

7．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为$\frac{1}{7}$．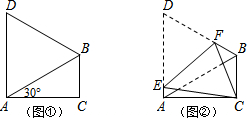

Answer 1

分析 在Rt△ABC中，设AB=2a，已知∠ACB=90°，∠CAB=30°，即可求得AB、AC的值，由折叠的性质知：DE=CE，可设出DE、CE的长，然后表示出AE的长，进而可在Rt△AEC中，由勾股定理求得AE、CE的值，即可求∠ACE的正弦值．

解答 解：∵△ABC中，∠ACB=90°，∠BAC=30°，设AB=2a，
∴AC=$\sqrt{3}$a，BC=a；
∵△ABD是等边三角形，
∴AD=AB=2a；
设DE=EC=x，则AE=2a-x；
在Rt△AEC中，由勾股定理，得：（2a-x）²+3a²=x²，
解得：x=$\frac{7}{4}$a；
∴AE=$\frac{1}{4}$a，EC=$\frac{7}{4}$a，
∴sin∠ACE=$\frac{AE}{CE}$=$\frac{1}{7}$；
故答案为：$\frac{1}{7}$．

点评 本题考查的是翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．