题目内容
在Rt△ABC中,∠C=90°,请你根据正弦的定义证明sin2A+sin2B=1.
考点:锐角三角函数的定义,勾股定理
专题:证明题
分析:先由勾股定理得出a2+b2=c2,再由正弦函数的定义可得sinA=
,sinB=
,然后代入sin2A+sin2B,即可证明.
| a |
| c |
| b |
| c |
解答:证明:在Rt△ABC中,∵∠C=90°,
∴a2+b2=c2,sinA=
,sinB=
,
∴sin2A+sin2B=(
)2+(
)2=
=1,
即sin2A+sin2B=1.
∴a2+b2=c2,sinA=
| a |
| c |
| b |
| c |
∴sin2A+sin2B=(
| a |
| c |
| b |
| c |
| a2+b2 |
| c2 |
即sin2A+sin2B=1.
点评:本题考查了锐角三角函数的定义,勾股定理,是基础题,比较简单.

练习册系列答案
相关题目
 如图,从一个大正方形中裁去面积为15cm2和24cm2的两个小正方形,求留下部分(即阴影部分)的面积.
如图,从一个大正方形中裁去面积为15cm2和24cm2的两个小正方形,求留下部分(即阴影部分)的面积.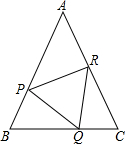 如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR.
如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR.