题目内容
用一根2m长的铁丝围成一个矩形,矩形的一条边长为x,面积为y,当x= 时,矩形的面积y最大.
考点:二次函数的最值
专题:
分析:先用x表示出另一边的长,再根据矩形的面积公式得出x、y的关系式,求出y的最大值即可.
解答:解:∵用一根2m长的铁丝围成一个矩形,矩形的一条边长为x,
∴另一条边长=
=1-x,
∴y=x(1-x)=-x2+x,
∴当x=-
=-
=
时,矩形的面积y最大.
故答案为:
.
∴另一条边长=
| 2-2x |
| 2 |
∴y=x(1-x)=-x2+x,
∴当x=-
| b |
| 2a |
| 1 |
| 2×(-1) |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的是二次函数的最值,熟知二次函数的顶点坐标是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
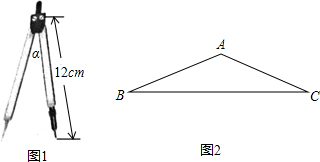 如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)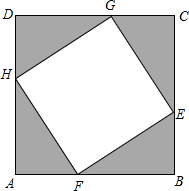 一张正方形纸板的边长为10cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分面积),设AH=BF=CG=DH=x(cm).阴影部分的面积为y(cm2),求,
一张正方形纸板的边长为10cm,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分面积),设AH=BF=CG=DH=x(cm).阴影部分的面积为y(cm2),求,