题目内容
2. 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,DE⊥AB.垂足为E,ED的延长线交BC的延长线于点F.
求证:AE=CF,∠A=∠F
证明:∵∠ACB=90°
(已知)∴DC⊥BC(垂直的定义)
∵BD为∠ABC的平分线,DE⊥AB,垂足为E(已知)
∴DC=DE角平分线上的点到角的两边的距离相等
∠DCF=∠DEA=90° (垂直的定义)
∵∠ADE=∠CDF对顶角相等
∴△ADE≌△FDCASA
∴AE=CF全等三角形的对应边相等
∠A=∠F全等三角形的对应角相等.
分析 由BD为∠ABC的平分线,DE⊥AB,垂足为E,根据角平分线的性质,即可证得DC=DE,继而证得△ADE≌△FDC,然后由全等三角形的性质,证得结论.
解答 证明:∵∠ACB=90°(已知)
∴DC⊥BC(垂直的定义),
∵BD为∠ABC的平分线,DE⊥AB,垂足为E(已知),
∴DC=DE(角平分线上的点到角的两边的距离相等),
∠DCF=∠DEA=90°(垂直的定义)
∵∠ADE=∠CDF(对顶角相等),
∴△ADE≌△FDC(ASA),
∴AE=CF(全等三角形的对应边相等)
∠A=∠F(全等三角形的对应角相等)
故答案为:角平分线上的点到角的两边的距离相等;对顶角相等;ASA;全等三角形的对应边相等;全等三角形的对应角相等.
点评 此题考查了全等三角形的判定与性质以及角平分线的性质.注意熟记各性质定理是解此题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
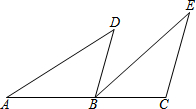 已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB.
已知:如图,点A、B、C在一条直线上,BD∥CE,AB=EC,BD=CB. 有理数a、b、c在数轴上的位置如图所示,求|a|、|-b|和-|-c|的值.
有理数a、b、c在数轴上的位置如图所示,求|a|、|-b|和-|-c|的值. 设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号.
设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号. 已知函数y=-x2+bx+2b-1的部分图象如图所示,求函数的解析式.
已知函数y=-x2+bx+2b-1的部分图象如图所示,求函数的解析式. 如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.
如图,AB是⊙O的直径,AB=2,分别以A,B为圆心,1为半径画弧与⊙O交于C,E,D,F,则阴影部分的面积是$\sqrt{3}$-$\frac{π}{3}$.