题目内容
1.在一次数学考试中,从某班随机抽取的10名学生得分如下:75、85、90、90、95、85、95、95、100、98.(1)求这10个得分的众数、中位数和平均数;
(2)若该班共有40名学生,估计此次考试的平均成绩约为多少.
分析 (1)先把数据由小到大排列,然后根据众数、中位数和平均数的定义求解;
(2)利用样本估计整体,用样本的平均数估计全班的平均数.
解答 解:(1)数据由小到大排列为:75、85、85、90、90、95、95、95、98、100,
所以这10个得分的众数为95,中位数为$\frac{90+95}{2}$=92.5,平均数=$\frac{1}{10}$(75+85+85+90+90+95+95+95+98+100)=90.8;
(2)估计此次考试的平均成绩约为90.8分.
点评 本题考查了中位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.也考查了用样本估计总体和众数.

练习册系列答案
相关题目
12.对函数y=x+1与函数y=-$\frac{1}{x}$,下列表述中正确的是( )
| A. | 两个函数图象都经过第四象限 | |
| B. | 两个函数图象有两个公共点 | |
| C. | 两个函数在自变量的取值范围内y都随x的增大而增大 | |
| D. | 在第二象限内,函数y=x+1的值小于函数y=-$\frac{1}{x}$的值 |
 在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点.
在平面直角坐标中,A为x轴上一点,过A点的直线L的解析式为y=kx-k(其中k为常数,且k≠0),B(3,m)为直线L上的另一点,C是y轴上一动点,过C点作直线L的平行线L′,连结AC,过B点作BD∥AC交于L′于D点. 如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.
如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环跳动,即第一次跳动到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…如此下去.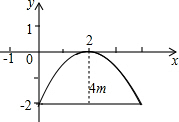 某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.
某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.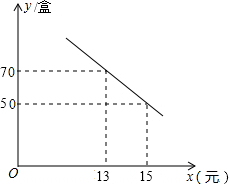 某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示.
某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示.