题目内容
15.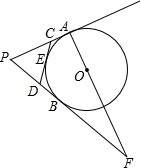 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.
分析 根据切线长定理易得PA=PB,CA=CE,DE=DB,再由△PCD的周长等于3r,即可求出PB的长,连接OB,首先证明△FBO∽△FAP,由相似三角形的性质可得$\frac{OB}{AP}$=$\frac{BF}{AF}$,设AF=x,OF=y,则$\frac{r}{\frac{3}{2}r}$=$\frac{x}{r+y}$,再在Rt△BFO中,OF2=OB2+BF2,即y2=x2+r2②,由①②可得x和r的关系,进而可求结果.
解答 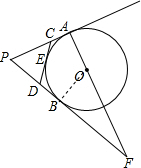 解:∵PA,PB切⊙O于A,B两点,CD切⊙O于点E,
解:∵PA,PB切⊙O于A,B两点,CD切⊙O于点E,
∴PA=PB,CA=CE,DE=DB,
∴△PCD的周长=PA+PB=2PA=3r,
∴PA=$\frac{3}{2}$r,
连接BO,
∵PA,PB切⊙O于A,B两点,
∴∠OBF=∠FAP=90°,
∴∠F+∠P=90°,∠F+∠BOF=90°
∴∠BPA=∠BOF,
∴△FBO∽△FAP,
∴$\frac{OB}{AP}$=$\frac{BF}{AF}$,
设BF=x,OF=y,
∴$\frac{r}{\frac{3}{2}r}$=$\frac{x}{r+y}$①,
在Rt△BFO中,OF2=OB2+BF2,
即y2=x2+r2②,
∴x=$\frac{12}{5}$r,y=$\frac{13}{5}$r,
∴$\frac{OA}{OF}$=$\frac{5}{13}$.
点评 本题考查了切线的性质、切线长定理、相似三角形的判定和性质、勾股定理,连接OB,构造直角三角形是解题的关键.

练习册系列答案
相关题目
6. 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 3 | D. | 无法确定 |
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.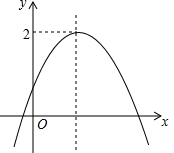 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论: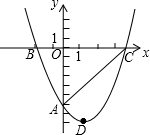 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.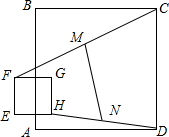 如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.
如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.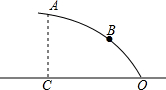 (1)先化简,再求值:$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$,其中x=2015.
(1)先化简,再求值:$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$,其中x=2015.