题目内容
5．已知a，b是方程x2-x-3=0的两个根，则代数式a2+b2的值为7．分析 根据根与系数的关系得到a+b=1，ab=-3，再把a2+b2变形为（a+b）2-2ab，然后利用整体代入思想计算．
解答 解：∵a，b是方程x2-x-3=0的两个根，
∴a+b=1，ab=-3，
∴a2+b2=（a+b）2-2ab=12-2×（-3）=7．
故答案为：7．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个解为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．
练习册系列答案
相关题目
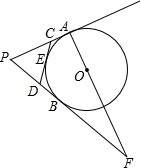如图，PA，PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于点C，D，连接AO并延长交PB的延长线于点F．若⊙O的半径为r，△PCD的周长等于3r，则$\frac{OA}{OF}$的值是$\frac{5}{13}$．
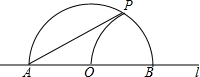如图，直线l上一点O，以O为圆心，任意长为半径画半圆，交l于A、B两点，再以B为圆心，OB的长为半径画弧交半圆于P，连AP，则sin∠PAB的值等于$\frac{1}{2}$．
13．下列运算正确的是（ ）
| A． | a2+a3=a5 | B． | a3•a2=a6 | C． | a0=1 | D． | 2015-1=-$\frac{1}{2015}$ |
10．关于函数y=2x，下列结论中正确的是（ ）
| A． | 函数图象都经过点（2，1） | B． | 函数图象都经过第二、四象限 | ||
| C． | y随x的增大而增大 | D． | 不论x取何值，总有y＞0 |
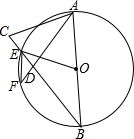如图，等腰三角形ABC中，BA=BC，以AB为直径作圆，交BC于点E，圆心为O．在EB上截取ED=EC，连接AD并延长，交⊙O于点F，连接OE、EF．
15．
过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．若AB=$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）
过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．若AB=$\sqrt{3}$，∠DCF=30°，则EF的长为（ ）| A． | 2 | B． | 3 | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |