题目内容
20.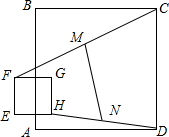 如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.
如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为$\sqrt{17}$a.
分析 因为题目没有确定正方形EFGH的位置,所以我们可以将正方形EFGH的位置特殊化,使点H与点A重合,重新作出图形,这样有利于我们解题,过点M作MO⊥ED与O,则可得出OM是梯形FEDC的中位线,从而可求出ON、OM,然后在RT△MON中利用勾股定理可求出MN.
解答 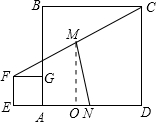 解:如图,将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED与O,则MO是梯形FEDC的中位线,
解:如图,将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED与O,则MO是梯形FEDC的中位线,
∴EO=OD=4a,MO=$\frac{1}{2}$(EF+CD)=4a.
∵点N、M分别是AD、FC的中点,
∴AN=ND=3a,
∴ON=OD-ND=4a-3a=a.
在Rt△MON中,MN2=MO2+ON2,即MN=$\sqrt{O{M}^{2}+O{N}^{2}}$=$\sqrt{16{a}^{2}+{a}^{2}}$=$\sqrt{17}$a.
故答案是:$\sqrt{17}$a.
点评 本题考查了梯形的中位线定理、正方形的性质及勾股定理的知识,属于综合性题目,对待这样既有动态因素又不确定位置的题目,一定要将位置特殊化,这样不影响结果且解题过程简单,同学们要学会在以后的解题中利用这种思想.

练习册系列答案
相关题目
5.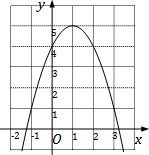 如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )
如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )
 如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )
如图是二次函数y=-x2+2x+4的图象,使y≤4成立的x的取值范围是( )| A. | 0≤x≤2 | B. | x≤0 | C. | x≥2 | D. | x≤0或x≥2 |
10.关于函数y=2x,下列结论中正确的是( )
| A. | 函数图象都经过点(2,1) | B. | 函数图象都经过第二、四象限 | ||
| C. | y随x的增大而增大 | D. | 不论x取何值,总有y>0 |
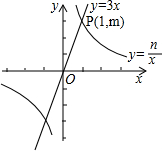 如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1.
如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1.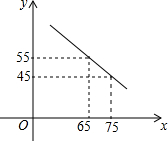 某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.
某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.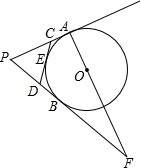 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.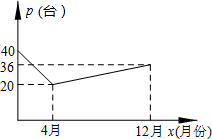 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.