题目内容
2.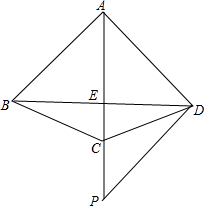 如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
分析 (1)直接利用等腰三角形的性质结合互余的定义得出∠BDC=∠PDC;
(2)首先过点C作CM⊥PD于点M,进而得出△CPM∽△APD,求出EC的长即可得出答案.
解答  (1)证明:∵AB=AD,AC平分∠BAD,
(1)证明:∵AB=AD,AC平分∠BAD,
∴AC⊥BD,
∴∠ACD+∠BDC=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC+∠BDC=90°,
∵PD⊥AD,
∴∠ADC+∠PDC=90°,
∴∠BDC=∠PDC;
(2)解:过点C作CM⊥PD于点M,
∵∠BDC=∠PDC,
∴CE=CM,
∵∠CMP=∠ADP=90°,∠P=∠P,
∴△CPM∽△APD,
∴$\frac{CM}{AD}$=$\frac{PC}{PA}$,
设CM=CE=x,
∵CE:CP=2:3,
∴PC=$\frac{3}{2}$x,
∵AB=AD=AC=1,
∴$\frac{x}{1}$=$\frac{\frac{3}{2}x}{\frac{3}{2}x+1}$,
解得:x=$\frac{1}{3}$,
故AE=1-$\frac{1}{3}$=$\frac{2}{3}$.
点评 此题主要考查了相似三角形的判定与性质以及等腰三角形的性质等知识,正确得出△CPM∽△APD是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )
| A. | 1:4 | B. | 4:1 | C. | 1:2 | D. | 2:1 |
10.袋内装有标号分别为1、2、3、4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{5}{16}$ | C. | $\frac{7}{16}$ | D. | $\frac{1}{2}$ |
17.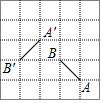 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
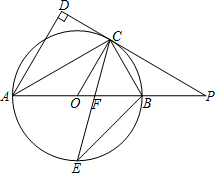 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.