题目内容
12.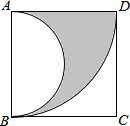 如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是2π(结果保留π).
如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是2π(结果保留π).
分析 根据题意有S阴影部分=S扇形BAD-S半圆BA,然后根据扇形的面积公式:S=$\frac{n{πR}^{2}}{360}$和圆的面积公式分别计算扇形和半圆的面积即可.
解答 解:根据题意得,S阴影部分=S扇形BAD-S半圆BA,
∵S扇形BAD=$\frac{90π{•4}^{2}}{360}$=4π
S半圆BA=$\frac{1}{2}$•π•22=2π,
∴S阴影部分=4π-2π=2π.
故答案为2π.
点评 此题考查了扇形的面积公式:S=$\frac{n{πR}^{2}}{360}$,其中n为扇形的圆心角的度数,R为圆的半径),或S=$\frac{1}{2}$lR,l为扇形的弧长,R为半径.

练习册系列答案
相关题目
2.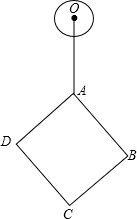 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,在旋转过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )| A. | 3次 | B. | 4次 | C. | 5次 | D. | 6次 |
20.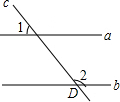 如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )
 如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为( )| A. | 150° | B. | 130° | C. | 100° | D. | 50° |
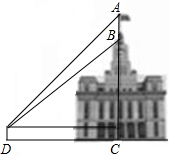 如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为7.2m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为7.2m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.
如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.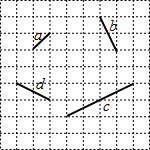 如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( ) 一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.
一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.