题目内容
19.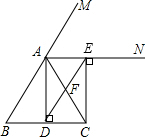 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.连接DE交AC于F.
已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.连接DE交AC于F.(1)求证:四边形ADCE为矩形;
(2)求证:DF∥AB,DF=$\frac{1}{2}$AB.
分析 (1)由AB=AC,得∠B=∠ACB,又有外角及角平分线的性质可得AN∥BC,再由垂直关系即可得出结论.
(2)由矩形的对角线相等且互相平分,得出∠FDC=∠FCD=∠B,即可DF∥AB,再由中位线定理可得DF=$\frac{1}{2}$AB.
解答  解:
解:
(1)证明:
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,∠ABC=∠ACB,
又∠MAC=∠ABC+∠ACB=2∠ACB,
又AN平分∠MAC,
∴∠NAC=∠MAN=∠ACB,
∵∠MAN+∠CAN+∠BAD+∠CAD=180°,
∴∠DAE=∠CAD+∠CAN=$\frac{1}{2}$×180°=90°,
又CE⊥AN,AD⊥BC,
∴∠ADC=∠AEC=90°,
∴四边形ADCE为矩形;
(2)证明:∵四边形ADCE为矩形,
对角线DE与AC相交于点F,
∴F是AC的中点,
∵D是BC的中点,
∴DF为△ABC的中位线,
∴DF=$\frac{1}{2}$AB.
点评 本题主要考查了矩形的判断和性质、平行线的判定、三角形中位线定理的运用及三角形外角的性质和角平分线的性质等,熟练掌握矩形的各种判断方法是解题的关键.

练习册系列答案
相关题目
4.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.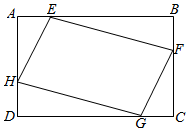 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )| A. | 5$\sqrt{5}$ | B. | 10$\sqrt{5}$ | C. | 10$\sqrt{3}$ | D. | 15$\sqrt{3}$ |
 如图,若∠1=∠D=38°,∠C和∠D互余,则∠B=128°.
如图,若∠1=∠D=38°,∠C和∠D互余,则∠B=128°.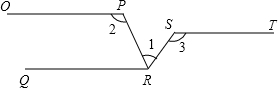 如图所示,OP∥QR∥ST,若∠2=120°,∠3=130°,则∠1=70度.
如图所示,OP∥QR∥ST,若∠2=120°,∠3=130°,则∠1=70度.