题目内容
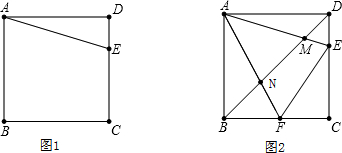
12.课题学习问题背景1 甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,
(1)①在图中画出旋转后的图形;
②图1中,与线段AE垂直的线段是AK⊥AE,说明你的理由.
问题背景2 如图2,在正方形ABCD中,∠EAF=45°,点F为BC上一点,点E为DC上一点,∠EAF的两边AE、AF分别与直线BD交于点M、N,连接EF,继续探索时,甲认为:线段BF、EF和DE之间存在着关系式EF=BF+DE;乙认为△CEF的周长是一个恒定不变的值;丙认为:线段BN、MN和DM之间存在着关系式BN2+DM2=MN2
(2)请你对甲、乙、丙三人中一个结论进行研究,作出判断,并说明你的理由.
分析 (1)根据图形旋转前后所构成的两图形全等画出图形即可;
(2)①选择甲,延长CB到K,使BK=DE,连AK,由图形旋转的性质可得△AKB≌△AED,可得出∠KAF=∠FAE,进而可得出△AKF≌△AEF,由全等三角形的性质及BK=DE可得出EF=BF+DE;
②选择乙,延长CB到K,使BK=DE,连AK,由图形旋转的性质可得△AKB≌△AED,由全等三角形的性质可得到△AKF≌△AEF,再根据BK=DE即可得出△CEF周长为定值;
③选择丙,在AK上截取AG=AM,连接BG,GN,由图形旋转的性质可得△ABG≌△ADM,△GAN≌△NAM,再由勾股定理即可得出BN2+DM2=MN2.
解答 解:画图如图1,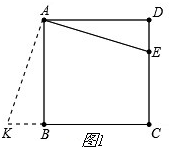
延长CB至K,使BK=DE,
∵四边形ABCD是正方形,
∴AD=AB,∠ADE=∠ABK=∠BAD=90°,
∴△ADE≌△ABK,
∴∠DAE=∠BAK,
∴∠EAK=∠BAK+∠BAE=∠DAK+∠BAE=∠BAD=90°,
∴AK⊥AE.
故答案为AK⊥AE.
(2)选择甲发现:
证明:如图2,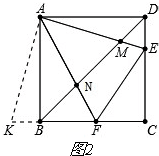
延长CB到K,使BK=DE,连AK,则△AKB≌△AED,
∵∠BAF+∠DAE=45°,
∴∠KAF=45°,
∴∠KAF=∠FAE.
∵AK=AE,AF=AF,
∴△AKF≌△AEF.
∴KF=EF.
又∵BK=DE,
∴EF=BF+DE
选择乙发现:
证明:如图2,
延长CB到K,使BK=DE,连AK,则△AKB≌△AED
∵∠BAF+∠DAE=45°,
∴∠KAF=45°,
∴∠KAF=∠FAE.
∵AK=AE,AF=AF,
∴△AKF≌△AEF.
∴KF=EF.
又∵BK=DE,
∴EF=BF+DE
△CEF周长=CF+CE+EF
=CF+CE+(BF+DE)
=(CF+BF)+(CE+DE)
=BC+DC=2a(定值)
选择丙发现:
证明:如图3,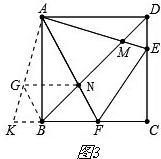
在AK上截取AG=AM,连接BG,GN.
∵AG=AM,AB=AD,∠KAB=∠EAD,
∴△ABG≌△ADM,
∴BG=DM,∠ABG=∠ADB=45°.
又∵∠ABD=45°,
∴∠GBD=90°.
∵∠BAF+∠DAE=45°,
∴∠KAF=45°,
∴∠KAF=∠FAE.
又∵AG=AM,AN=AN,
∴△GAN≌△NAM.
∴NG=MN,
∵∠GBD=90°,
∴BG2+BN2=NG2,
∴BN2+DM2=MN2.
综上所述:甲、乙、丙三名同学的发现都是正确的.
点评 此题是四边形综合题,主要考查了正方形的性质,全等三角形的性质和判定,垂直的判定方法,解本题的关键是三角形的全等的判定.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案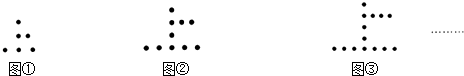
| A. | 36 | B. | 38 | C. | 42 | D. | 50 |
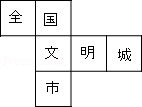 在市委、市府的领导下,全市人民齐心协力,将我市成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“全”字所在的面相对的字应是( )
在市委、市府的领导下,全市人民齐心协力,将我市成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“全”字所在的面相对的字应是( )| A. | 文 | B. | 明 | C. | 城 | D. | 市 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (n-1)2 | B. | n2 | C. | (n+1)2 | D. | (n+2)2 |