题目内容
13．古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性，若把第一个三角数记为a1，第二个三角数记为a2…，第n个三角数记为an，计算a1+a2，a2+a3，a3+a4，…由此推算a2015+a2016=20162．分析 先求出a1+a2，a2+a3，a3+a4，的值，根据规律可以推算a2015+a2016．
解答 解：∵a1+a2=4=22，a2+a3=9=32，a3+a4=16=42，…
由此推算由此推算a2015+a2016=20162
故答案为20162．
点评 本题考查规律型：数字变化类，解题的关键是学会从一般到特殊的探究方法，找到规律后即可解决问题，属于中考常考题型．
练习册系列答案
相关题目
4．图中是正方体的展开图的共有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．在x=-4，0，-1.2，π中满足不等式组$\left\{\begin{array}{l}{x＜2}\\{2（x+1）＞-2}\end{array}\right.$的x值是（ ）
| A． | -4和0 | B． | -4和-1.2 | C． | 0和π | D． | -1.2和0 |
李祥用棋子摆出了四个不同的图案（如图），请你仔细观察其中的规律，然后画出按此规律排列的第五个图案，看一看第五个图案中一共有多少个棋子，你能归纳出一个一般性的结论吗？
2．古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记为a1，第二个三角数记为a2，…，第n个三角数记为an，则an-1+an=（ ）（ ）
| A． | （n-1）2 | B． | n2 | C． | （n+1）2 | D． | （n+2）2 |
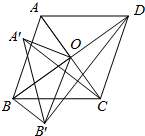已知：菱形ABCD的对角线AC，BD相交于点O，将△AOB绕点O逆时针方向旋转得到△A′OB′，旋转角为α（0°＜α＜90°），连接A′C，B′D，B′B，且AC=6，AD=5．