题目内容
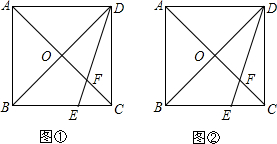
4.如图,四边形ABCD为矩形,E是BC延长线上一点,AE交CD于点G,F是AE上一点,并且AC=CF=EF,∠AEB=15°.(1)求∠ACF的度数;
(2)证明:矩形ABCD为正方形.
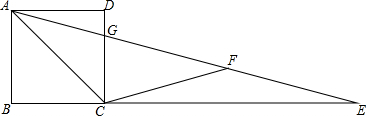
分析 (1)利用矩形的性质可得∠DAG=∠AEB=15°,利用外角的性质和等腰三角形的性质可得∠AFC与∠CAF的度数,可得∠ACF;
(2)由∠DAG=15°,∠FAC=30°,易得∠DAC=45°,可得∠ACD=∠DAC=45°,由等腰三角形的判定可得AD=CD,由正方形的判定定理证得结论.
解答 解:(1)∵四边形ABCD为矩形,
∴AD∥BC,∠D=90°,
∴∠DAG=∠AEB=15°,
∵CF=EF,
∴∠FCE=∠AEB=15°,
∴∠AFC=∠FCE+∠AEB=30°,
∵AC=CF,
∴∠FAC=∠AFC=30°,
∴∠ACF=18O°-∠FAC-∠AFC=120°;
(2)由(1)知∠DAG=15°,∠FAC=30°,
∴∠DAC=∠DAG+∠FAC=45°,
∵∠D=90°,
∴∠ACD=∠DAC=45°,
∴AD=CD,
∴矩形ABCD为正方形.
点评 本题主要考查了矩形的性质和正方形的判定定理,利用角的关系是解答此题的关键.

练习册系列答案
相关题目
 某公园准备用如图所示的材料给一块矩形的场地铺地面
某公园准备用如图所示的材料给一块矩形的场地铺地面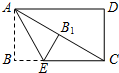 如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.
如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.