题目内容
17.将正方形纸片以适当的方式折叠一次,沿折痕剪开后得到两块小纸片,用这两块小纸片拼接成一个新的多边形(不重叠、无缝隙),给出以下结论:①可以拼成等腰直角三角形;
②可以拼成对角互补的四边形;
③可以拼成五边形;
④可以拼成六边形.
其中所有正确结论的序号是①②③④.
分析 分剪开的两个部分是等腰直角三角形和梯形和全等的梯形三种情况,将正方形的边重合或剪开的相等的边重合作出图形即可得解.
解答 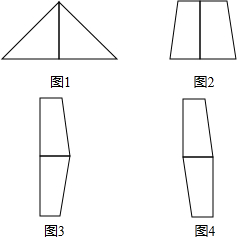 解:如图1,剪成两个等腰直角三角形时可以拼成等腰直角三角形;
解:如图1,剪成两个等腰直角三角形时可以拼成等腰直角三角形;
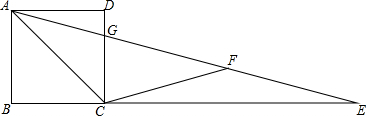
如图2,剪成两个梯形可以拼成对角互补的四边形;
如图3,图4,剪成两个全等的梯形可以拼成五边形和六边形;
所以,正确结论的序号①②③④.
故答案为:①②③④.
点评 本题考查了图形的简拼,此类题目,关键在于确定出重叠的边和图形的方法,难点在于考虑问题要全面.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
12.下列运算正确的是( )
| A. | a3-a2=a | B. | (a2)3=a5 | C. | a4•a=a5 | D. | 3x+5y=8xy |
 如图,在△ABC中,∠A=60°,BD⊥AC,CE⊥AB,垂足为D、E,试说明DE=$\frac{1}{2}$BC.
如图,在△ABC中,∠A=60°,BD⊥AC,CE⊥AB,垂足为D、E,试说明DE=$\frac{1}{2}$BC.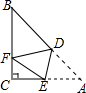 如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).
如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).