题目内容
19.(1)解不等式组:$\left\{\begin{array}{l}{2x>x-2}\\{\frac{2x+1}{3}>x}\end{array}\right.$(2)化简:$\frac{2x}{{x}^{2}-1}-\frac{1}{x-1}$.
分析 (1)分别解出两不等式的解集,再求其公共解.
(2)把分式的分子分母分别分解因式,然后进行约分即可.
解答 解:(1)$\left\{\begin{array}{l}{2x>x-2①}\\{\frac{2x+1}{3}>x②}\end{array}\right.$,
由①得 x>-2,
由②得x<1,
所以,原不等式组的解集为-2<x<1.
(2)$\frac{2x}{{x}^{2}-1}-\frac{1}{x-1}$
=$\frac{2x}{(x+1)(x-1)}$-$\frac{1}{x-1}$
=$\frac{2x}{(x+1)(x-1)}$-$\frac{x+1}{(x+1)(x-1)}$
=$\frac{x-1}{(x+1)(x-1)}$
=$\frac{1}{x+1}$.
点评 本题主要考查了一元一次不等式组解集的求法和分式的化简,解不等式组的简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
12.下列运算正确的是( )
| A. | a3-a2=a | B. | (a2)3=a5 | C. | a4•a=a5 | D. | 3x+5y=8xy |
 写出图中直线所对应的函数关系.
写出图中直线所对应的函数关系.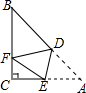 如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).
如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).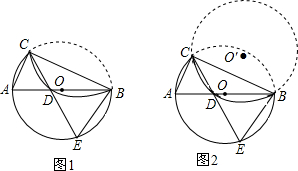
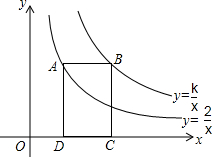 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,且它的面积为3,则k=5.
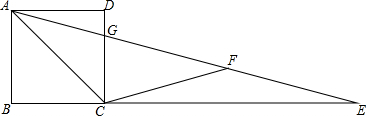
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,点C,D在x轴上.若四边形ABCD为矩形,且它的面积为3,则k=5.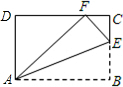 如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为32cm.
如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为32cm.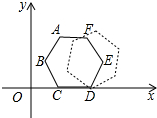 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.