题目内容

5．在Rt△ABC中，∠C=90°，AC=3，BC=4，那么sinB的值是（　　）
A．$\frac{3}{4}$B．$\frac{4}{3}$C．$\frac{4}{5}$D．$\frac{3}{5}$

分析 先根据勾股定理求出AB的长，再运用锐角三角函数的定义解答．

解答 解：∵在△ABC中，∠C=90°，AC=3，BC=4，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴sinB=$\frac{AC}{AB}$=$\frac{3}{5}$．
故选D．

点评 本题考查了锐角三角函数的定义，勾股定理．正确记忆定义是解题关键．

练习册系列答案
相关题目
15．有两个十分喜欢探究的同学小明和小芳，他们善于将所做的题目进行归类，下面是他们的探究过程．
（1）解题与归纳
①小明摘选了以下各题，请你帮他完成填空．$\sqrt{2^2}$=2； $\sqrt{5^2}$=5； $\sqrt{6^2}$=6；$\sqrt{0^2}$=0； $\sqrt{{{（{-3}）}^2}}$=3； $\sqrt{{{（{-6}）}^2}}$=6；
②归纳：对于任意数a，有$\sqrt{a^2}$=|a|=$\left\{\begin{array}{l}{a（a＞0）}\\{0（a=0）}\\{-a（a＜0）}\end{array}\right.$
③小芳摘选了以下各题，请你帮她完成填空．$（\sqrt{4}{）^2}$=4； $（\sqrt{9}{）^2}$=9； $（\sqrt{25}{）^2}$=25；$（\sqrt{36}{）^2}$=36；$（\sqrt{49}{）^2}$=49； $（\sqrt{0}{）^2}$=0；
④归纳：对于任意非负数a，有$（\sqrt{a}{）^2}$=a
（2）应用
根据他们归纳得出的结论，解答问题．
数a，b在数轴上的位置如图所示，化简：$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{（a-b）^{2}}$-$（\sqrt{b-a}{）^2}$．
16．如图，AB∥CD，AD=BC，猜想∠BCD与∠ADC有什么关系？请说明理由．
13．如图①，正方形ABCD中，点O是对角线AC的中点，点P是线段AO上（不与A，O重合）的一个动点，过点P作PE⊥PB且PE交边CD于点E．
（1）求证：PB=PE．
（2）如图②，若正方形ABCD的边长为2，过E作EF⊥AC于点F，在P点运动的过程中，PF的长度是否发生变化？若不变，试求出这个不变的值；若变化，请说明理由．
（3）如图③，用等式表示线段PC，PA，CE之间的数量关系．
20．写出一个解为x＞-1的一元一次不等式x+1＞0（答案不唯一）．
10．下列方程中一定是关于x的一元二次方程是（　　）
A．ax2+bx+c=0B．$\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0C．3（x+1）2=2（x+1）D．x2-x（x+7）=0
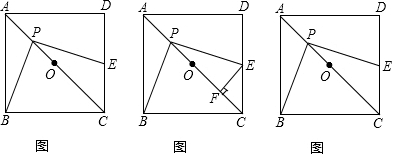
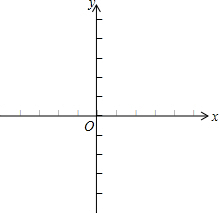17．使用五点法画出二次函数y=x2-2x-3的图象．
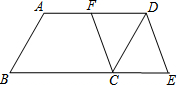14．如图，在?ABCD中，F是AD的中点，延长BC到点E，使CE=$\frac{1}{2}$BC，连接DE，CF．
（1）求证：DE=CF；
（2）若AB=4，AD=6，∠B=60°，求DE的长．
15．
（1）指出小明的作业从哪一步开始出现的错误，请更正过来，并计算出正确结果；
（2）若a，b是不等式组$\left\{\begin{array}{l}{2x＞0}\\{x-3＜0}\end{array}\right.$的整数解（a＜b），求上题分式的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网