题目内容
20.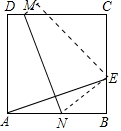 如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.
如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.
分析 连接MA,ME,由翻折可得,AN=NE,AM=EM,设AB=AD=2x,AN=a,在Rt△BEN中,a2=(2x-a)2+x2,解得:a=$\frac{5}{4}$x,在Rt△ADM和Rt△EMC中,CM=2x-b,由勾股定理得出方程(2x-b)2+x2=(2x)2+b2,解得:DM=b=$\frac{1}{4}$x,由梯形ADMN的面积求出x=1,得出AB=2;因为两个梯形的高相等,所以面积比即为边长(DM+AN)与(BN+CM)的比,即可得出结果.
解答 解:连接MA,ME,如图所示: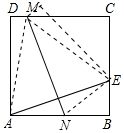 由翻折可得,AN=NE,AM=EM,
由翻折可得,AN=NE,AM=EM,
设AB=AD=2x,AN=a,
在Rt△BEN中,a2=(2x-a)2+x2,
解得:a=$\frac{5}{4}$x,
在Rt△ADM,设DM=b,则AM2=(2x)2+b2,
在Rt△EMC中,CM=2x-b,则EM2=(2x-b)2+x2,
∴(2x-b)2+x2=(2x)2+b2,
解得:DM=b=$\frac{1}{4}$x,
∵梯形ADMN的面积=$\frac{1}{2}$(DM+AN)•AD=$\frac{3}{2}$
∴$\frac{1}{2}$($\frac{1}{4}$x+$\frac{5}{4}$x)•2x=$\frac{3}{2}$,
解得:x=±1(负值舍去),
∴x=1,
∴AB=2,DM=$\frac{1}{4}$,AN=$\frac{5}{4}$,BN=$\frac{3}{4}$,CM=$\frac{7}{4}$,
梯形ADMN与梯形BCMN的面积之比=$\frac{DM+AN}{BN+CM}$═$\frac{\frac{1}{4}+\frac{5}{4}}{\frac{3}{4}+\frac{7}{4}}$=$\frac{3}{5}$;
故答案为:2;$\frac{3}{5}$.
点评 本题考查了翻折变换的性质、正方形的性质、勾股定理、梯形面积的计算;熟练掌握翻折变换和正方形的性质,由勾股定理得出方程是解决问题的关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 62500 | B. | 1000 | C. | 500 | D. | 250 |
| A. | -2016 | B. | $\frac{1}{2016}$ | C. | -$\frac{1}{2016}$ | D. | 2016 |
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | 3(x+1)2=2(x+1) | D. | x2-x(x+7)=0 |
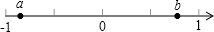 有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.
有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程. “折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺.
“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺. 如图,已知点A,B.
如图,已知点A,B.