题目内容
14.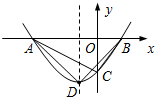 如图,已知二次函数y=$\frac{2}{3}$(x+3)(x-1)的图象与x轴交于点A、B,与y轴交于点C,顶点坐标为D.则△ABC与△ABD的面积之比是( )
如图,已知二次函数y=$\frac{2}{3}$(x+3)(x-1)的图象与x轴交于点A、B,与y轴交于点C,顶点坐标为D.则△ABC与△ABD的面积之比是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{8}$ |
分析 首先求出A和B点坐标,即可求出AB的长,然后求出点C和顶点坐标,最后根据三角形面积公式求出面积比.
解答 解:令y=$\frac{2}{3}$(x+3)(x-1)=0,
解得x1=-3,x2=1,
∴AB=4,
∴A点坐标为(-3,0),B点坐标为(1,0),
∵y=$\frac{2}{3}$(x+3)(x-1),
∴y=$\frac{2}{3}$x2+$\frac{4}{3}$x-2=$\frac{2}{3}$(x+1)2-$\frac{8}{3}$,
∴C点坐标为(0,-2),D点坐标为(-1,-$\frac{8}{3}$),
∵S△ABC=$\frac{1}{2}$×AB×OC=$\frac{1}{2}$×4×2=4,S△ABD=$\frac{1}{2}$×AB×OD=$\frac{1}{2}$×4×$\frac{8}{3}$=$\frac{16}{3}$,
∴S△ABC:S△ABD=4:$\frac{16}{3}$=$\frac{3}{4}$,
故选B.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是求出顶点坐标以及C点的坐标,此题难度不大.

练习册系列答案
相关题目
19.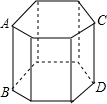 如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
 如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )
如图,直六棱柱的底面是边长为4cm的正六边形,AB为8cm,则此直六棱柱左视图的面积为( )| A. | 32$\sqrt{3}$cm2 | B. | 32cm2 | C. | 64cm2 | D. | 16$\sqrt{3}$cm2 |
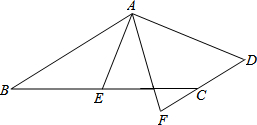 已知,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.
已知,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.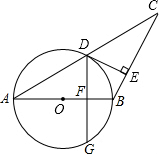 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.