题目内容
3.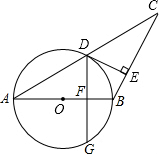 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.(1)求证:DE是⊙O的切线;
(2)作DG⊥AB交⊙O于G,垂足为F,求证DE=$\frac{1}{2}$DG.
分析 (1)连接OD,只要证明OD⊥DE即可.
(2)连结BD,根据AAS证得△ADF≌△CDE得出DE=DF,然后根据垂径定理得DF=$\frac{1}{2}$DG,即可证得结论.
解答 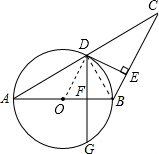 (1)证明:连结OD.
(1)证明:连结OD.
∵OA=OD,
∴∠A=∠ADO,
∵BA=BC,
∴∠A=∠C,
∴∠ADO=∠C,
∴DO∥BC,
∵DE⊥BC,
∴DO⊥DE,
又点D在⊙O上,
∴DE是⊙O的切线;
(2)解:连结BD,
∵AB是圆O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴AD=DC,
在△ADF和△CDE中,
$\left\{\begin{array}{l}{∠A=∠C}\\{∠AFD=∠CED=90°}\\{AD=DC}\end{array}\right.$
∴△ADF≌△CDE(AAS),
∴DE=DF,
∵直径AB⊥弦DG,由垂径定理得DF=$\frac{1}{2}$DG,
∴DE=$\frac{1}{2}$DG.
点评 本题考查了切线的判定三角形全等的判定和性质,圆周角定理等腰三角形的性质等.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直是证明切线的常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.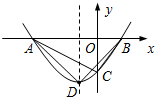 如图,已知二次函数y=$\frac{2}{3}$(x+3)(x-1)的图象与x轴交于点A、B,与y轴交于点C,顶点坐标为D.则△ABC与△ABD的面积之比是( )
如图,已知二次函数y=$\frac{2}{3}$(x+3)(x-1)的图象与x轴交于点A、B,与y轴交于点C,顶点坐标为D.则△ABC与△ABD的面积之比是( )
 如图,已知二次函数y=$\frac{2}{3}$(x+3)(x-1)的图象与x轴交于点A、B,与y轴交于点C,顶点坐标为D.则△ABC与△ABD的面积之比是( )
如图,已知二次函数y=$\frac{2}{3}$(x+3)(x-1)的图象与x轴交于点A、B,与y轴交于点C,顶点坐标为D.则△ABC与△ABD的面积之比是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{8}$ |
3.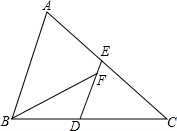 如图,在△ABC中,D、E分别是BC、AC上的中点,且DE∥AB,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( )
如图,在△ABC中,D、E分别是BC、AC上的中点,且DE∥AB,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( )
 如图,在△ABC中,D、E分别是BC、AC上的中点,且DE∥AB,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( )
如图,在△ABC中,D、E分别是BC、AC上的中点,且DE∥AB,BF平分∠ABC,交DE于点F,若BC=8,则DF的长是( )| A. | 2 | B. | 3 | C. | $\frac{5}{2}$ | D. | 4 |
 如图,CD⊥AB于点D,FE⊥AB于点E,∠1=∠2,试判断∠AGD与∠ACB的关系,并说明理由.
如图,CD⊥AB于点D,FE⊥AB于点E,∠1=∠2,试判断∠AGD与∠ACB的关系,并说明理由.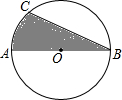 如图,⊙O的半径为6cm,AB是⊙O的直径,BC是弦,∠ABC=30°,则图中阴影部分的面积为6π+9$\sqrt{3}$cm2(结果用无理数表示)
如图,⊙O的半径为6cm,AB是⊙O的直径,BC是弦,∠ABC=30°,则图中阴影部分的面积为6π+9$\sqrt{3}$cm2(结果用无理数表示)