题目内容
一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为( )
| A、8 | B、9 | C、10 | D、12 |
考点:多边形内角与外角
专题:
分析:设正多边形的每个外角的度数为x,与它相邻的内角的度数为4x,根据邻补角的定义得到x+4x=180°,解出x=36°,然后根据多边形的外角和为360°即可计算出多边形的边数.
解答:解:设正多边形的每个外角的度数为x,与它相邻的内角的度数为4x,依题意有
x+4x=180°,
解得x=36°,
这个多边形的边数=360°÷36°=10.
故选:C.
x+4x=180°,
解得x=36°,
这个多边形的边数=360°÷36°=10.
故选:C.
点评:本题考查了多边形的外角定理:多边形的外角和为360°.也考查了邻补角的定义.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
甲、乙两列火车长分别是150米和200米,它们相向行驶在平行的轨道上,已知甲车上某位乘客测得乙车在他窗口外经过的时间是10秒,那么乙车上的乘客看见甲车在他窗口经过的时间是( )
| A、5秒 | B、7.5秒 |
| C、8.5秒 | D、10秒 |
设f(x)=x2-2011x+2011,f(x)表示关于x的函数,如f(0)=02-2011•0+2011=2011,f(m)=m2-2011m+2011,若m≠n,f(m)=f(n),则f(m+n)=( )
| A、0 | B、2011 |
| C、-2011 | D、不能求出 |
 如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则∠E为( )
如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则∠E为( )| A、25° | B、30° |
| C、35° | D、45° |
已知二次函数y=ax2+bx+c图象开口向上,与x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
| A、abc<0 |
| B、b=2a |
| C、a+b+c=0 |
| D、2a+b=0 |
 如图,AB是⊙O的直径,∠ABC=45°,AC=AB,BC交⊙O于点D.
如图,AB是⊙O的直径,∠ABC=45°,AC=AB,BC交⊙O于点D.
 (1)解方程:6x2-x-12=0
(1)解方程:6x2-x-12=0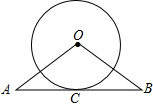 如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长.
如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长. 如图,已知△ABC中,点D、E分别在边AB、AC上,DE∥BC,若AD=4,BD=2,DE=3,那么BC=
如图,已知△ABC中,点D、E分别在边AB、AC上,DE∥BC,若AD=4,BD=2,DE=3,那么BC=