题目内容
1.比$\frac{4}{7}$大且比$\frac{6}{7}$小的分数有( )| A. | 一个 | B. | 两个 | C. | 无数个 | D. | 不存在 |
分析 依据分数的基本性质,将两个分数分子和分母同时扩大若干倍,介于它们中间的分数就会有无数个,从而可以作出正确选择.
解答 解:因为$\frac{4}{7}=\frac{40}{70}$,
$\frac{6}{7}=\frac{60}{70}$,
则大于$\frac{40}{70}$而小于$\frac{60}{70}$的数有:
$\frac{60}{70}>\frac{59}{70}$…>$\frac{41}{70}>\frac{40}{70}$;
同理,将两个分数同时扩大若干倍数,
就会得到无数个介于它们中间的数.
故选:C.
点评 考查了有理数大小比较,解答此题的关键是:将两个分数分子和分母同时扩大若干倍,就会得到无数个介于它们中间的数.

练习册系列答案
相关题目
9.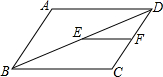 如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
 如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | 8 | D. | 9 |
6.若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是( )
| A. | -9 | B. | -3 | C. | 3 | D. | -3或3 |
13.点A的坐标是(-1,-3),则点A在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.不透明的袋子中装有10个黑球、1个白球,它们除颜色外无其它差别,随机从袋子中摸出一个球,则( )
| A. | 这个球一定是黑球 | B. | 事先能确定摸到什么颜色的球 | ||
| C. | 这个球可能是白球 | D. | 摸到黑球、白球的可能性大小一样 |
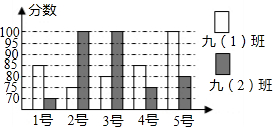 某中学开展“唱红歌”歌唱比赛,九年级(1)班、九年级(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
某中学开展“唱红歌”歌唱比赛,九年级(1)班、九年级(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示: