题目内容
1．
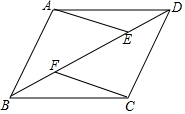如图，?ABCD中，点E、F在BD上，且BF=DE．请连接AF、CE，并证明四边形AFCE是平行四边形．
分析 如图，连接AF、CE，连接AC交BD于点O．只要证明OA=OC，OE=OF即可解决问题．
解答 证明：如图，连接AF、CE，连接AC交BD于点O．
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵BF=DE，
∴OF=OE，
∵OA=OC，
∴四边形AECF是平行四边形．
点评 本题考查平行四边形的性质和判定，解题的关键是熟练掌握平行四边形的判定，属于中考常考题型．
练习册系列答案
相关题目
9．
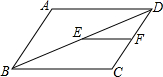如图，在平行四边形ABCD中，AD=16，点E、F分别是BD、CD的中点，则EF的长为（ ）
如图，在平行四边形ABCD中，AD=16，点E、F分别是BD、CD的中点，则EF的长为（ ）| A． | 6 | B． | $\frac{16}{3}$ | C． | 8 | D． | 9 |
16．
已知有理数a、b在数轴上的位置如图，则化简|a-b|+|a+b|的结果为（ ）
已知有理数a、b在数轴上的位置如图，则化简|a-b|+|a+b|的结果为（ ）| A． | -2a | B． | 2a | C． | 2b | D． | -2b |
6．若正比例函数y=kx的图象经过点A（k，9），且经过第一、三象限，则k的值是（ ）
| A． | -9 | B． | -3 | C． | 3 | D． | -3或3 |
13．点A的坐标是（-1，-3），则点A在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
14．
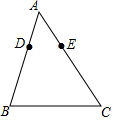如图，在△ABC中，已知D、E分别是AB、AC边上的点，且AD=3，AB=8，AC=10，若△ADE与△ABC相似，则AE的长为（ ）
如图，在△ABC中，已知D、E分别是AB、AC边上的点，且AD=3，AB=8，AC=10，若△ADE与△ABC相似，则AE的长为（ ）| A． | $\frac{15}{4}$ | B． | $\frac{4}{15}$或$\frac{12}{5}$ | C． | $\frac{15}{4}$或$\frac{12}{5}$ | D． | $\frac{5}{12}$ |