题目内容
12.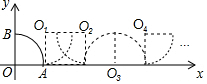 如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )| A. | (16+4π,0) | B. | (14+4π,2) | C. | (14+3π,2) | D. | (12+3π,0) |
分析 由点A(2,0),B(0,2),得到OA=2,OB=2,∠AOB=90°,根据弧长的计算公式得到$\widehat{AB}$的长度=$\frac{90•π×{2}^{\;}}{180}$=π,得到O1O2=$\widehat{AB}$的长度=π,于是得到结论.
解答 解:∵点A(2,0),B(0,2),
∴OA=2,OB=2,∠AOB=90°,
∴$\widehat{AB}$的长度=$\frac{90•π×{2}^{\;}}{180}$=π,
∵将扇形AOB沿x轴正方向做无滑动的滚动,
∴O1O2=$\widehat{AB}$的长度=π,
∴点O1(2,2),点O2(2+π,2),点O3(4+π,0),点O4(6+π,2),…,
∵10÷3=3…1,
∴O10的(14+3π,2).
故选C.
点评 本题考查了规律型:点的坐标,主要考查了从滚动中找出规律,根据规律确定坐标对应点是解本题的关键.

练习册系列答案
相关题目
7.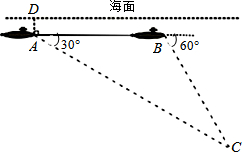 如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
 如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )| A. | 2000米 | B. | 4000米 | C. | 2000$\sqrt{3}$米 | D. | (2000$\sqrt{3}$+500)米 |
 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF 如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.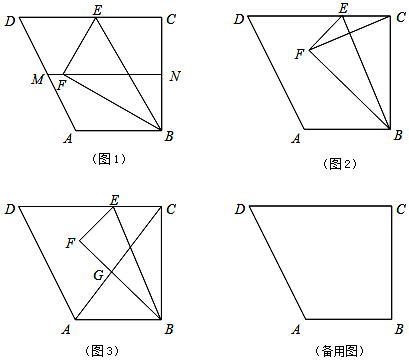
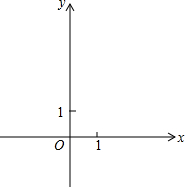 如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
 如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).