题目内容
17.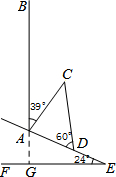 如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.
如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.(1)求∠DAC的度数;
(2)求这棵大树折断前高是多少米?(结果精确到个位)($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
分析 (1)如果延长BA交EF于点G,那么BG⊥EF,∠CAE=180°-∠BAC-∠EAG,∠BAC的度数以及确定,只要求出∠GAE即可.直角三角形GAE中∠E的度数已知,那么∠EAG的度数就能求出来了,∠CAE便可求出;
(2)求树折断前的高度,就是求AC和CD的长,如果过点A作AH⊥CD,垂足为H.有∠CDA=60°,通过构筑的直角三角形AHD和ACH便可求出AD、CD的值.
解答 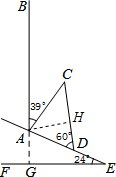 解:(1)延长BA交EF于点G.
解:(1)延长BA交EF于点G.
在Rt△AGE中,∠E=24°,
∴∠GAE=66°.
又∵∠BAC=39°,
∴∠CAE=180°-66°-39°=75°.
(2)过点A作AH⊥CD,垂足为H.
在△ADH中,∠ADC=60°,AD=4,cos∠ADC=$\frac{DH}{AD}$,∴DH=2.
sin∠ADC=$\frac{AH}{AD}$,∴AH=2$\sqrt{3}$.
在Rt△ACH中,
∵∠C=180°-75°-60°=45°,CH=AH=2$\sqrt{3}$,
∴AC=2$\sqrt{6}$,CH=AH=2$\sqrt{3}$.
∴AB=AC+CD=2$\sqrt{6}$+2$\sqrt{3}$+2≈10(米).
答:这棵大树折断前高约10米.
点评 本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
8.下列图形中,轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.某超市设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“5元”、“10元”、“20元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回),并根据两个小球所标总金额换取等值的购物券.某顾客刚好消费200元,则该顾客所获得购物券的金额不低于20元的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
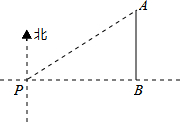 如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.
如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.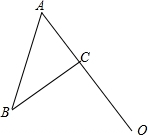 如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4.
如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4. 如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?
如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?