题目内容
12. 已知,在△ABC中∠ACB=90°,AC=BC,点P在△ABC内,且PA=3,PB=1,PC=2,求证:∠BPC=135°.
已知,在△ABC中∠ACB=90°,AC=BC,点P在△ABC内,且PA=3,PB=1,PC=2,求证:∠BPC=135°.
分析 把△APC绕点C逆时针旋转90°得到△BDC,根据旋转的性质可得△PCD是等腰直角三角形,BD=AP,∠APC=∠BDC,根据等腰直角三角形的性质求出PD,∠PDC=45°,然后利用勾股定理逆定理判断出△PBD是直角三角形,∠DPB=90°,再求出∠BPC即可得解.
解答 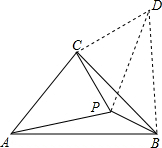 解:如图,把△APC绕点C逆时针旋转90°得到△BDC,
解:如图,把△APC绕点C逆时针旋转90°得到△BDC,
由旋转的性质得,△PCD是等腰直角三角形,BD=AP=3,∠APC=∠BDC,
所以PD=$\sqrt{2}$PC=2$\sqrt{2}$,∠PDC=45°,
∵PD2+PB2=(2$\sqrt{2}$)2+12=9,
PA2=32=9,
∴PD2+PB2=BD2,
∴△PBD是直角三角形,∠DPB=90°,
∴∠BPC=90°+45°=135°,
∴∠BPC=135°.
故答案是:135°.
点评 本题考查了旋转的性质,勾股定理逆定理,等腰直角三角形的判定与性质,熟记各性质并作辅助线构造出等腰直角三角形和直角三角形是解题的关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
4.关于x,y的方程组$\left\{\begin{array}{l}x+py=0\\ x+y=3\end{array}\right.$的解是$\left\{\begin{array}{l}x=1\\ y=▲\end{array}$,其中y的值被盖住了,不过仍能求出p,则p的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
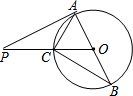 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于C,连结BC、AC,若∠PAC=30°,AC=4,则BC=4$\sqrt{3}$.
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于C,连结BC、AC,若∠PAC=30°,AC=4,则BC=4$\sqrt{3}$. 解不等式2(x+4)-5<3(x+1)+4,并把解集在如图所示的数轴上表示出来.
解不等式2(x+4)-5<3(x+1)+4,并把解集在如图所示的数轴上表示出来.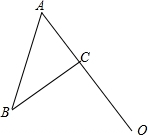 如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4.
如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4.