题目内容
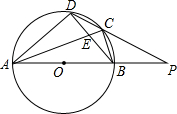 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2
| 2 |
考点:相似三角形的判定与性质,圆周角定理
专题:计算题
分析:(1)由DC2=CE•CA和∠ACD=∠DCE,可判断△CAD∽△CDE,得到∠CAD=∠CDE,再根据圆周角定理得∠CAD=∠CBD,所以∠CDB=∠CBD,于是利用等腰三角形的判定可得BC=DC;
(2)连结OC,如图,设⊙O的半径为r,先证明OC∥AD,利用平行线分线段成比例定理得到
=
=2,则PC=2CD=4
,然后证明△PCB∽△PAD,利用相似比得到
=
,再利用比例的性质可计算出r的值.
(2)连结OC,如图,设⊙O的半径为r,先证明OC∥AD,利用平行线分线段成比例定理得到
| PC |
| CD |
| PO |
| OA |
| 2 |
4
| ||
| 3r |
| r | ||
6
|
解答:(1)证明:∵DC2=CE•CA,
∴
=
,
而∠ACD=∠DCE,
∴△CAD∽△CDE,
∴∠CAD=∠CDE,
∵∠CAD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC;
(2)解:连结OC,如图,设⊙O的半径为r,
∵CD=CB,
∴
=
,
∴∠BOC=∠BAD,
∴OC∥AD,
∴
=
=
=2,
∴PC=2CD=4
,
∵∠PCB=∠PAD,∠CPB=∠APD,
∴△PCB∽△PAD,
∴
=
,即
=
,
∴r=4,
即⊙O的半径为4.
∴
| DC |
| CE |
| CA |
| DC |
而∠ACD=∠DCE,
∴△CAD∽△CDE,

∴∠CAD=∠CDE,
∵∠CAD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC;
(2)解:连结OC,如图,设⊙O的半径为r,
∵CD=CB,
∴
 |
| CD |
 |
| CB |
∴∠BOC=∠BAD,
∴OC∥AD,
∴
| PC |
| CD |
| PO |
| OA |
| 2r |
| r |
∴PC=2CD=4
| 2 |
∵∠PCB=∠PAD,∠CPB=∠APD,
∴△PCB∽△PAD,
∴
| PC |
| PA |
| PB |
| PD |
4
| ||
| 3r |
| r | ||
6
|
∴r=4,
即⊙O的半径为4.
点评:本题考查了相似三角形的判定与性质:三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有事可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.也考查了圆周角定理.

练习册系列答案
相关题目
下列各式运算正确的是( )
| A、3x+3y=6xy |
| B、7x-5x=2x2 |
| C、16y2-7y2=9 |
| D、19a2b-9ba2=10a2b |
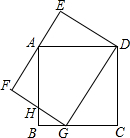 如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5. 已知三角形的中线,通常把中线延长一倍,构造全等三角形.如图,△ABC中,AD是中线,AD也是角平分线,求证:△ABC是等腰三角形.
已知三角形的中线,通常把中线延长一倍,构造全等三角形.如图,△ABC中,AD是中线,AD也是角平分线,求证:△ABC是等腰三角形.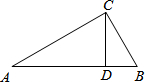 如图,在Rt△ABC中,∠C=90°,CD⊥AB,D为垂足,且BC:AC=2:3,那么BD:AD的值为
如图,在Rt△ABC中,∠C=90°,CD⊥AB,D为垂足,且BC:AC=2:3,那么BD:AD的值为 如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,
如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,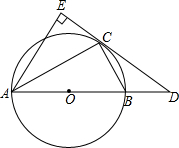 如图,AB是⊙O的直径,D是AB的延长线上的一点,点C在⊙O上,AE⊥DC交
如图,AB是⊙O的直径,D是AB的延长线上的一点,点C在⊙O上,AE⊥DC交