题目内容
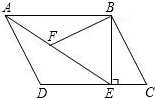 如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D.
如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D.(1)求证:△ABF∽△EAD;
(2)若AB=4,AD=3,∠BAE=30°,求BF的长.
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:(1)可通过证明∠BAF=∠AED,∠AFB=∠D,证得△ABF∽△EAD;
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.通过解直角三角形ABE求出AE的长,这样就能求出BF的长了.
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.通过解直角三角形ABE求出AE的长,这样就能求出BF的长了.
解答: (1)证明:∵在平行四边形ABCD中,AB∥CD,
(1)证明:∵在平行四边形ABCD中,AB∥CD,
∴∠BAF=∠AED.
又∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
又∠BAE=30°,AB=4,
∴AE=
=
=
∵由(1)知,△ABF∽△EAD,
∴
=
.即
=
,
∴BF=
.
 (1)证明:∵在平行四边形ABCD中,AB∥CD,
(1)证明:∵在平行四边形ABCD中,AB∥CD,∴∠BAF=∠AED.
又∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
又∠BAE=30°,AB=4,
∴AE=
| AB |
| cos30° |
| 4 | ||||
|
8
| ||
| 3 |
∵由(1)知,△ABF∽△EAD,
∴
| BF |
| AD |
| AB |
| AE |
| BF |
| 3 |
| 4 | ||||
|
∴BF=
3
| ||
| 2 |
点评:本题主要考查了相似三角形的判定和性质,同时也用到了平行四边形的性质.相似三角形相似多边形的特殊情形,它沿袭相似多边形的定义,从对应边的比相等和对应角相等两方面下定义;反过来,两个三角形相似也有对应角相等,对应边的比相等.

练习册系列答案
相关题目
经专家估算,南海内的油气资源约合15000亿美元,用科学记数法表示数字15000是( )
| A、15×103 |
| B、1.5×104 |
| C、1.5×103 |
| D、1.5×105 |
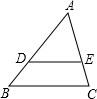 如图,已知AD•AC=AE•AB,求证:DE∥BC.
如图,已知AD•AC=AE•AB,求证:DE∥BC.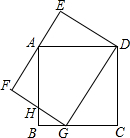 如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.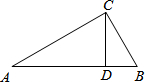 如图,在Rt△ABC中,∠C=90°,CD⊥AB,D为垂足,且BC:AC=2:3,那么BD:AD的值为
如图,在Rt△ABC中,∠C=90°,CD⊥AB,D为垂足,且BC:AC=2:3,那么BD:AD的值为 如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于
如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于