题目内容
15. 已知AD⊥BC,CE⊥AB,AB=BC.
已知AD⊥BC,CE⊥AB,AB=BC.(1)求证:△ABD≌△CBE;
(2)求证:EF=FD.
分析 (1)直接利用垂直的定义得出∠BEC=∠BDA,进而利用AAS,得出△ABD≌△CBE;
(2)利用全等三角形的性质结合全等三角形的判定方法得出△AEF≌△CDF(ASA),进而得出答案.
解答 证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BEC=∠BDA,
在△ABD和△CBE中
∵$\left\{\begin{array}{l}{∠ADB=∠CEB}\\{∠B=∠B}\\{AB=BC}\end{array}\right.$,
∴△ABD≌△CBE(AAS);
(2)∵△ABD≌△CBE,
∴BD=BE,∠A=∠C,
∴AE=DC,
在△AEF和△CDF中
∵$\left\{\begin{array}{l}{∠A=∠C}\\{AE=DC}\\{∠AEF=∠CDF}\end{array}\right.$,
∴△AEF≌△CDF(ASA),
∴EF=FD.
点评 此题主要考查了全等三角形的判定与性质,正确掌握全等三角形的判定方法是解题关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
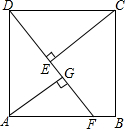 如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.
如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.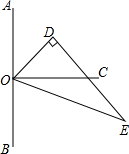 如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.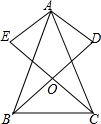 如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.
如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.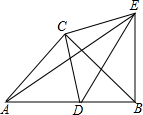 如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=∠90°,D为AB边上一点.
如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=∠90°,D为AB边上一点.