题目内容
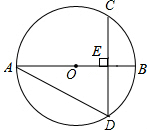 如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2.
如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2.(1)求⊙O半径;
(2)求弦CD的长.
考点:垂径定理,勾股定理
专题:
分析:(1)连接OD,设⊙O的半径为r,则OE=r-2,再根据圆周角定理得出∠DOE=60°,由直角三角形的性质可知OD=2OE,由此可得出r的长;
(2)再Rt△OED中根据勾股定理求出DE的长,进而可得出结论.
(2)再Rt△OED中根据勾股定理求出DE的长,进而可得出结论.
解答: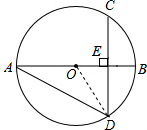 解:(1)连接OD,设⊙O的半径为r,则OE=r-2,
解:(1)连接OD,设⊙O的半径为r,则OE=r-2,
∵∠BAD=30°,
∴∠DOE=60°,
∵CD⊥AB,
∴CD=2DE,∠ODE=30°,
∴OD=2OE,即r=2(r-2),解得r=4;
(2)∵由(1)知r=4,BE=2,
∴OE=4-2=2,
∴DE=
=
=2
,
∴CD=2DE=4
.
 解:(1)连接OD,设⊙O的半径为r,则OE=r-2,
解:(1)连接OD,设⊙O的半径为r,则OE=r-2,∵∠BAD=30°,
∴∠DOE=60°,
∵CD⊥AB,
∴CD=2DE,∠ODE=30°,
∴OD=2OE,即r=2(r-2),解得r=4;
(2)∵由(1)知r=4,BE=2,
∴OE=4-2=2,
∴DE=
| OD2-OE2 |
| 42-22 |
| 3 |
∴CD=2DE=4
| 3 |
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,回答下列问题:
如图,回答下列问题: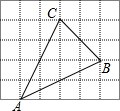 如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB=
如图,网格中的每个小正方形的边长都是1,△ABC的每个顶点都在网格格点处,则sin∠CAB=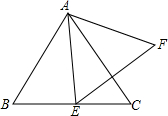 如图,点E为边长为4的等边△ABC的BC边上一动点(点E不与B、C重合),以AE为边作等边△AEF,求△AEF面积的最小值.
如图,点E为边长为4的等边△ABC的BC边上一动点(点E不与B、C重合),以AE为边作等边△AEF,求△AEF面积的最小值.
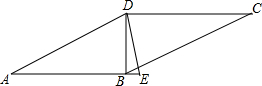 如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.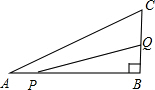 在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2?
在△ABC中.∠B=90°,AB=6cm,BC=5cm,点P从点A开始,沿AB边向点B以1cm/s的速度移动,点Q从点B开始,沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发.经过多少秒后,△PBQ的面积等于8cm2?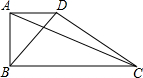 有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由.
有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由.