Question

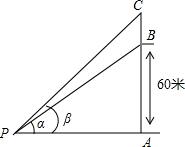如图，在高为60米的楼顶B处，安装一块广告牌BC，小明用仪器在点P处测得楼顶B的仰角为α，广告牌顶端的仰角为β，其中tanα=

3

4

，tanβ=

4

5

，求广告牌的高度BC．

Answer 1

考点：解直角三角形的应用-仰角俯角问题

专题：

分析：设BC的高度为x米，则AC=AB+BC=（x+60）米，再由已知条件tanα=

3

4

，tanβ=

4

5

，建立关于x的方程，解方程即可得到x的值，即广告牌的高度．

解答：解：设BC的高度为x米，则AC=AB+BC=（x+60）米，
∵tanα=

3

4

，
∴

AB

PA

=

3

4

，
∵AB=60米，
∴PA=80米，
∵tanβ=

4

5

，
∴

AC

PA

=

4

5

，
即

x+60

80

=

4

5

，
解得：x=4．
答：广告牌的高度BC是4米．

点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．