题目内容
6.意大利著名数学家斐波那契发现有这样一组数:1,1,2,3,5,8,13,….其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值分别构造正方形,再从左到右分别取前2个、前3个、前4个、前5个正方形拼成如图所示的若干个长方形并按序依次记为①、②、③、④、….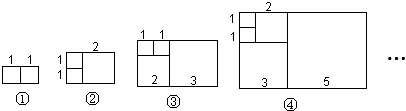
每个长方形的周长如表所示:
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
(2)若按此规律继续拼长方形,则序号为⑩的长方形周长是466.
分析 结合图形分析表格中图形的周长,①的周长为:2×(1+2),②的周长为:2×(2+3),③的周长为:2×(3+5),④的周长为:2×(5+8),…由此可推出第n个长方形的宽为第n-1个长方形的长,第n个长方形的长为第n-1个长方形的长和宽的和,长方形的周长是前面两个长方形的周长和,由此规律解决问题即可.
解答 解:(1)由分析知:第①个长方形的周长为6=(1+2)×2;
第②个长方形的周长为10=(2+3)×2;
第③个长方形的周长为x=(3+5)×2=16;
第④个长方形的周长为y=(5+8)×2=26;
(2)若按此规律继续拼成长方形,则
第⑤个长方形的周长为42=(8+13)×2;
第⑥个长方形的周长为68=(13+21)×2;
第⑦个长方形的周长为110=(21+34)×2;
第⑧个长方形的周长为178=(34+55)×2;
第⑨个长方形的周长为288=(55+89)×2;
∴序号为⑩的长方形周长是(89+144)×2=466;
故答案为:(1)16,26;(3)466.
点评 此题考查图形的变化规律,要想得到长方形的周长规律,应先找长方形长、宽的变换规律.分析图形中的长和宽,然后结合图表中长方形的周长即可得出长方形周长的变换规律.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
16.我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示是( )
| A. | 0.675×105 | B. | 67.5×103 | C. | 6.75×104 | D. | 6.75×105 |
17.下列方程是一元一次方程的是( )
| A. | $\frac{2}{y}$=1 | B. | 3x+2y=0 | C. | x2-l=0 | D. | x=3 |
18.为了创建“全国文明城市”,我校志愿者小组成员从学校出发,在学校门口东西方向的道路上进行义务保洁.规定向东行为正,向西行为负,已知某志愿者一个下午的七次行走记录如表所示(单位:千米):
(1)该志愿者保洁结束时是否回到出发地点?如果没有,那么距离出发点多少千米?
(2)在第六次保洁时离出发地点最远;
(3)若每千米平均用时15分钟,则该志愿者完成这次保洁任务一共用时多少小时?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| +1 | -1.1 | +2 | +0.7 | -1 | +1.2 | -3 |
(2)在第六次保洁时离出发地点最远;
(3)若每千米平均用时15分钟,则该志愿者完成这次保洁任务一共用时多少小时?
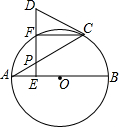 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,延长EP交$\widehat{AC}$于点F,且在射线EP上找到一点D使得DC=DP.
如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,延长EP交$\widehat{AC}$于点F,且在射线EP上找到一点D使得DC=DP.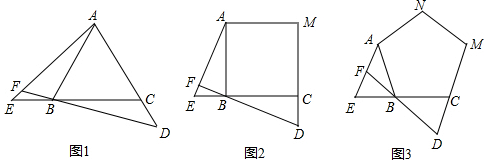
 如图△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=15°,则∠DGB=65°.
如图△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=15°,则∠DGB=65°.