Question

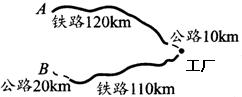如图所示，某工厂与A、B两地由公路、铁路相连．这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地销售，公路运价为1.5元/（吨•千米），铁路运价为1.2元/（吨•千米），这两次运输共支出公路运费15000元，铁路运费97200元．
（1）分别求出该工厂购买的原料重量与制成的产品重量；
（2）若此工厂在生产过程中还需付出各种生产成本费用共80万元，求出该工厂此次经营的利润？
（经营利润=销售款-原料费用-运输费-生产成本）

Answer 1

考点：二元一次方程组的应用

专题：

分析：（1）设该工厂购买的原料重量为x吨，制成的产品重量为y吨，根据两次运输共支出公路运费15000元，铁路运费97200元，列方程组求解；
（2）根据经营利润=销售款-原料费用-运输费-生产成本，代入求解．

解答：解：（1）设该工厂购买的原料重量为x吨，制成的产品重量为y吨，
由题意得，

120×1.2x+110×1.2y=97200 10×1.5x+20×1.5y=15000

，
解得：

x=400 y=300

．
答：该工厂购买的原料重量为400吨，制成的产品重量为300吨；

（2）利润=8000×300-400×1000-15000-97200-800000=1087800（元）．
答：该工厂此次经营的利润为1087800元．

点评：本题考查了二元一次方程组的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程组求解．