题目内容
已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
(1)如图1,若∠COF=28°,则∠BOE= °;
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的关系是否仍然成立?如成立,请说明理由.
(3)在图3中,若∠COF=65°,在∠BOE=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD+∠AOF=
(∠BOE-∠BOD)?若存在,请求出∠BOD的度数;若不存在,请说明理由.
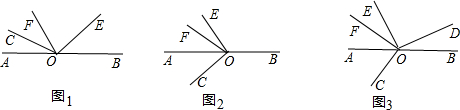
(1)如图1,若∠COF=28°,则∠BOE=
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的关系是否仍然成立?如成立,请说明理由.
(3)在图3中,若∠COF=65°,在∠BOE=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD+∠AOF=
| 1 |
| 2 |

考点:角的计算,角平分线的定义
专题:
分析:利用角的平分线和角的和差关系计算;首先由角平分线和∠COF的度数求出∠AOE,再根据邻补角关系求出∠BOE.
解答:解:(1)∵∠COF=28°,∠COE=90°,
∴∠EOF=90°-28°=62°,
∵OF平分∠AOE,∴∠AOE=2∠EOF=124°,
∴∠BOE=180°-∠AOE=56°;
故∠BOE=56°;
(2)∠BOE=2∠COF仍然成立;理由如下:
∵∠COE=90°,
∴∠EOF=90°-∠COF,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°-2∠COF,
∴∠BOE=180°-∠AOE=180°-(180°-2∠COF)=2∠COF;
(3)存在;
∵∠COF=65°,∠COE=90°,
∴∠BOE=130°,∠EOF=25°,
∵OF平分∠AOE,
∴∠AOF=∠EOF=25°,
∵2∠BOD+∠AOF=
(∠BOE-∠BOD),
即2∠BOD+25°=
(130°-∠BOD),
解得∠BOD=16°.
∴∠EOF=90°-28°=62°,
∵OF平分∠AOE,∴∠AOE=2∠EOF=124°,
∴∠BOE=180°-∠AOE=56°;
故∠BOE=56°;
(2)∠BOE=2∠COF仍然成立;理由如下:
∵∠COE=90°,
∴∠EOF=90°-∠COF,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°-2∠COF,
∴∠BOE=180°-∠AOE=180°-(180°-2∠COF)=2∠COF;
(3)存在;
∵∠COF=65°,∠COE=90°,
∴∠BOE=130°,∠EOF=25°,
∵OF平分∠AOE,
∴∠AOF=∠EOF=25°,
∵2∠BOD+∠AOF=
| 1 |
| 2 |
即2∠BOD+25°=
| 1 |
| 2 |
解得∠BOD=16°.
点评:此题考查了角的计算,关键是利用角平分线认真观察图形,找出角的和差关系是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
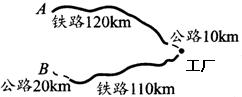 如图所示,某工厂与A、B两地由公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地销售,公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15000元,铁路运费97200元.
如图所示,某工厂与A、B两地由公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地销售,公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15000元,铁路运费97200元.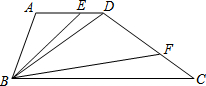 如图,在梯形ABCD中,AD∥BC,AD=AB,∠ABC=2∠C,E与F分别为边AD与DC上的两点,且有∠EBF=∠C.
如图,在梯形ABCD中,AD∥BC,AD=AB,∠ABC=2∠C,E与F分别为边AD与DC上的两点,且有∠EBF=∠C.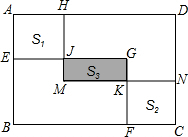 如图,在矩形ABCD中,矩形EBFG通过平移变换得到矩形HMND,点E、F、N、H都在矩形ABCD的边上.若BE=3,BF=4,4S3=S1+S2,且四边形AEJH和CFKN都是正方形,则图中空白部分的面积为
如图,在矩形ABCD中,矩形EBFG通过平移变换得到矩形HMND,点E、F、N、H都在矩形ABCD的边上.若BE=3,BF=4,4S3=S1+S2,且四边形AEJH和CFKN都是正方形,则图中空白部分的面积为