题目内容
10.下列关系式是否成立(0<α<90°),请说明理由.(1)sinα+cosα≤1;
(2)sin2α=2sinα.
分析 (1)利用三角函数的定义和三角形的三边关系得到该结论不成立;
(2)举出反例进行论证.
解答 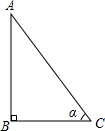 解:(1)该不等式不成立,理由如下:
解:(1)该不等式不成立,理由如下:
如图,在△ABC中,∠B=90°,∠C=α.
则sinα+cosα=$\frac{AB}{AC}$+$\frac{BC}{AC}$=$\frac{AC+BC}{AC}$>1,故sinα+cosα≤1不成立;
(2)该等式不成立,理由如下:
假设α=30°,则sin2α=sin60°=$\frac{\sqrt{3}}{2}$,2sinα=2sin30°=2×$\frac{1}{2}$=1,
∵$\frac{\sqrt{3}}{2}$≠1,
∴sin2α≠2sinα,即sin2α=2sinα不成立.
点评 本题考查了同角三角函数的关系.解题的关键是掌握锐角三角函数的定义和特殊角的三角函数值.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
18.数轴上A,B,C三点所表示的数分别为a,b,c,且点C在线段AB上,若|a|=|b|,且线段AC的长度是线段CB的3倍,则下列有关a,b,c的式子,表示正确的是( )
| A. | |c|=$\frac{1}{2}$|b| | B. | |c|=$\frac{1}{3}$|b| | C. | |c|=$\frac{1}{4}$|b| | D. | |c|=$\frac{3}{4}$|b| |
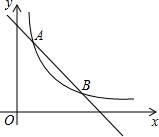 如图,在直角坐标系中,直线y=6-x与函数y=$\frac{5}{x}$(x>0)的图象交于A、B,设A(x1,y1),那么长为x1,宽为y1的矩形的面积和周长分别是5、12.
如图,在直角坐标系中,直线y=6-x与函数y=$\frac{5}{x}$(x>0)的图象交于A、B,设A(x1,y1),那么长为x1,宽为y1的矩形的面积和周长分别是5、12.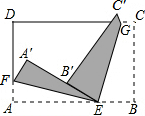 将一张长方形纸面按如图所示的方式进行折叠,使点A落至点A′处,点B落至B′处,并且E、A′、B′在同一条直线上,试确定EF与EG有怎样的位置关系,并说明理由.
将一张长方形纸面按如图所示的方式进行折叠,使点A落至点A′处,点B落至B′处,并且E、A′、B′在同一条直线上,试确定EF与EG有怎样的位置关系,并说明理由.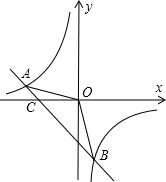 如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.
如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.