题目内容
5.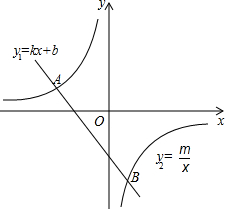 如图,已知A(-2,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$(m≠0)的图象的两个交点,则当0<y1≤y2时,x的取值范围是-2≤x<-1.
如图,已知A(-2,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$(m≠0)的图象的两个交点,则当0<y1≤y2时,x的取值范围是-2≤x<-1.
分析 利用待定系数法即可求得函数的解析式;一次函数的值小于反比例函数的值的x的取值范围,就是对应的一次函数的图象在反比例函数的图象的上边的自变量的取值范围.
解答 解:把A(-2,2)代入y2=$\frac{m}{x}$(m≠0)得:m=-4,
则反比例函数的解析式是:y2=-$\frac{4}{x}$;
把y=-4代入y2=-$\frac{4}{x}$,得:x=n=1,
则B的坐标是(1,-4).
把A、B坐标代入y1=kx+b,
$\left\{\begin{array}{l}{-2k+b=2}\\{k+b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
则一次函数的解析式为y=-2x-2,
在与x轴的交点为(-1,0),
根据图象可知在第二象限内,使一次函数的函数值小于反比例函数的函数值的x的取值范围是:-2≤x<-1.
故则当0<y1≤y2时,x的取值范围是:-2≤x<-1.
故答案为-2≤x<-1.
点评 本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.

练习册系列答案
相关题目
13.在一张1:100的地图上1cm2的面积的地,其实际面积是( )
| A. | 10000cm2 | B. | 1000cm2 | C. | 10cm2 | D. | 100cm2 |
14. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.抛物线y=ax2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表:
从上表可知,方程ax2+bx+c=4解是-1或2.
| x | … | -2 | -1 | 0 | 1 | … |
| y | … | 0 | 4 | 6 | 6 | … |
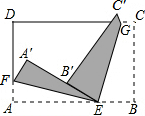 将一张长方形纸面按如图所示的方式进行折叠,使点A落至点A′处,点B落至B′处,并且E、A′、B′在同一条直线上,试确定EF与EG有怎样的位置关系,并说明理由.
将一张长方形纸面按如图所示的方式进行折叠,使点A落至点A′处,点B落至B′处,并且E、A′、B′在同一条直线上,试确定EF与EG有怎样的位置关系,并说明理由.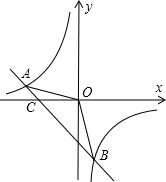 如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.
如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.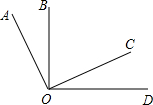 如图,∠AOC与∠BOD都是直角,若∠COD=30°,试求∠AOD,∠BOC的度数.
如图,∠AOC与∠BOD都是直角,若∠COD=30°,试求∠AOD,∠BOC的度数.