��Ŀ����
11��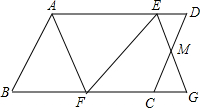 ��֪����ͼ����?ABCD�У�AB=8cm��BC=12cm����E��F�ֱ��DZ�BC��AD�ϵĶ��㣬��E���Fͬʱ��������E�ӵ�B��ʼ��2cm/s���ٶ����C�˶�����F�ӵ�D��ʼ��1cm/s���ٶ����A�˶���������һ���㵽���յ�ʱ����һ����Ҳ����ֹͣ�˶������˶�ʱ��Ϊt�룬��MΪCD���е㣬����FM���ӳ�����ֱ��BC�ڵ�G��
��֪����ͼ����?ABCD�У�AB=8cm��BC=12cm����E��F�ֱ��DZ�BC��AD�ϵĶ��㣬��E���Fͬʱ��������E�ӵ�B��ʼ��2cm/s���ٶ����C�˶�����F�ӵ�D��ʼ��1cm/s���ٶ����A�˶���������һ���㵽���յ�ʱ����һ����Ҳ����ֹͣ�˶������˶�ʱ��Ϊt�룬��MΪCD���е㣬����FM���ӳ�����ֱ��BC�ڵ�G����1����֤���ı���AEGFΪƽ���ı��Σ�
��2����գ�����B=60�㣺
�ٵ�t��ֵΪ2ʱ���ı���AEGFΪ���Σ�
�ڵ�t��ֵΪ4ʱ���ı���AEGFΪ���Σ�
���� ��1������ƽ���ı��ε����ʵó�AD��BC��AD=BC����һ��֤�á�EMD�ա�GCM���ó�DE=CG����һ���ó�AE=FG֤�ý��ۣ�
��2���ٵ���AFB=��CED=90��ʱ���ı���AEGFΪ���Σ����BF�����ó�t����ֵ���ɣ�
�ڵ�AE=AFʱ���ı���AEGFΪ���Σ���AH��BF������Ϊ��H�����AH����t��ʾ��HF��AE�����ù��ɶ����ó�AF������������ô𰸼��ɣ�
��� ��1��֤�������ı���ABCD��ƽ���ı��Σ�
��AD��BC��AD=BC��
���D=��MCG��
��MΪCD���е㣬
��DM=CM��
�ڡ�EMD�͡�GCM�У�
$\left\{\begin{array}{l}{��D=��MCG}\\{��DME=��GMC}\\{DM=CM}\end{array}\right.$��
���EMD�ա�GCM��AAS����
��DE=CG��
��AE=AD-DE=12-t��FG=BC+CG-BF=12+t-2t=12-t��
��AE=FG��
���ı���AEGF��ƽ���ı��Σ�
��2���ٵ���AFB=90��ʱ���ı���AEGFΪ���Σ�
�ߡ�B=60�㣬
���BAF=30�㣬
��BF=$\frac{1}{2}$AB=4cm
��t=4��2=2s��
�ڵ�AE=AFʱ���ı���AEGFΪ���Σ�
��ͼ��
��AH��BF��������H��
�ߡ�B=60�㣬AB=8
��BH=4��AH=4$\sqrt{3}$��
��HF=2t-4��
��AF=$\sqrt{A{H}^{2}+H{F}^{2}}$=$\sqrt{4{t}^{2}-16t+64}$��
�֡�AE=12-t��
��12-t=$\sqrt{4{t}^{2}-16t+64}$��
��ã�t1=4��t2=-$\frac{20}{3}$���������⣬��ȥ��
��˵�t��ֵΪ4ʱ���ı���AEGFΪ���Σ�
���� ���⿼��ƽ���ı��ε��ж������ʣ����ε��ж������ε��ж���������ȫ�ȵ��ж������ʣ�����֪ʶ֮�����ϵ����������ı��ε��й��ж�������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | 12 | B�� | 16 | C�� | 20��16 | D�� | 20 |
| A�� | ͨ���¶Ƚ���0�����£�������ˮ��� | |
| B�� | ���ⷭ��һ�����ijҳ����ҳ��ҳ�������� | |
| C�� | ��һö��ͨ���������ӣ����ϵ�һ����7�� | |
| D�� | ����ij���������£����Ϊ-150�� |
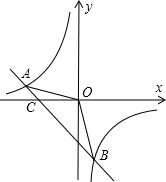 ��ͼ����֪��A��һ8��n����B��3��-8����һ�κ���y=kx+b��ͼ��ͷ���������$y=\frac{m}{x}$ͼ����������㣮
��ͼ����֪��A��һ8��n����B��3��-8����һ�κ���y=kx+b��ͼ��ͷ���������$y=\frac{m}{x}$ͼ����������㣮