题目内容
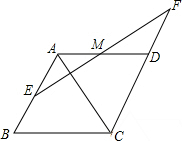 如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF交AD于M,交CD的延长线于点F.
如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF交AD于M,交CD的延长线于点F.(1)求证:EF、AD互相平分;
(2)若DF=2,求菱形ABCD的周长.
考点:菱形的性质,平行四边形的判定与性质
专题:
分析:(1)连接BD,根据菱形的对角线互相垂直可得AC⊥BD,然后求出EM∥BD,再判断出M是AD的中点,从而得证;
(2)判断出四边形FDBE是平行四边形,根据平行四边形的对边相等求出BE,再求出AB,然后根据菱形的周长公式进行计算即可得解.
(2)判断出四边形FDBE是平行四边形,根据平行四边形的对边相等求出BE,再求出AB,然后根据菱形的周长公式进行计算即可得解.
解答: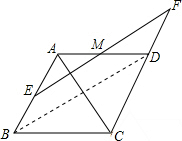 (1)证明:连接BD,
(1)证明:连接BD,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EM⊥AC,
∴EM∥BD,
∵E为AB的中点,
∴EM是△ABD的中位线,
∴M为AD的中点,EM=
BD.
∵EB∥FD,EM∥BD,
∴四边形FDBE是平行四边形,
∴EF=BD,
∴MF=EF-EM=BD-
BD=
BD,
∴EM=FM,
∴点M是EF的中点,
∴EF、AD互相平分;
(2)解:∵由(1)知,四边形FDBE是平行四边形,
∴FD=BE,
∵DF=2,
∴BE=2,
∴AB=2BE=2×2=4,
∴菱形ABCD的周长=4AB=4×4=16.
 (1)证明:连接BD,
(1)证明:连接BD,∵四边形ABCD是菱形,
∴AC⊥BD,
∵EM⊥AC,
∴EM∥BD,
∵E为AB的中点,
∴EM是△ABD的中位线,
∴M为AD的中点,EM=
| 1 |
| 2 |
∵EB∥FD,EM∥BD,
∴四边形FDBE是平行四边形,
∴EF=BD,
∴MF=EF-EM=BD-
| 1 |
| 2 |
| 1 |
| 2 |
∴EM=FM,
∴点M是EF的中点,
∴EF、AD互相平分;
(2)解:∵由(1)知,四边形FDBE是平行四边形,
∴FD=BE,
∵DF=2,
∴BE=2,
∴AB=2BE=2×2=4,
∴菱形ABCD的周长=4AB=4×4=16.
点评:本题考查了菱形的性质,主要利用了菱形的对角线互相垂直的性质,菱形的四条边都相等的性质.解答(1)题也可以利用全等三角形的性质进行证明.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
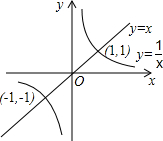 我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>
我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>| 1 |
| x |
| A、x>1 |
| B、-1<x<0 |
| C、x>1或-1<x<0 |
| D、以上都不对 |
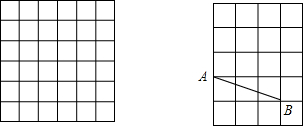
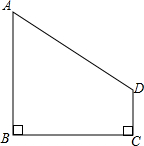 如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由.
如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由. 如图,在正方形内,以各边为半径画圆,所围成阴影部分的面积是S,求正方形的边长a(用含字母S,π的式子表示).
如图,在正方形内,以各边为半径画圆,所围成阴影部分的面积是S,求正方形的边长a(用含字母S,π的式子表示). 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB=( )
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB=( ) 如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.
如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.