题目内容
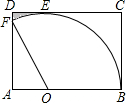 如图,在矩形纸片ABCD中,AB=9cm,BC=6cm,O在AB上,若以O为圆心,画弧与BC相切于B,与CD相切于点E,交AD于点F,连结FO,若把扇形BOF剪下,围成一个圆锥的侧面(不计接口尺寸).求:
如图,在矩形纸片ABCD中,AB=9cm,BC=6cm,O在AB上,若以O为圆心,画弧与BC相切于B,与CD相切于点E,交AD于点F,连结FO,若把扇形BOF剪下,围成一个圆锥的侧面(不计接口尺寸).求:(1)圆锥的底面半径;
(2)阴影部分的面积.
考点:切线的性质,扇形面积的计算,圆锥的计算
专题:计算题
分析:(1)连接OE,由CD与圆O相切,利用切线的性质得到OE垂直于CD,且OE为圆的半径,由AB-OB求出OA的长,在直角三角形AOF中,利用勾股定理求出AF的长,利用锐角三角函数定义求出cos∠AOF的值,确定出∠AOF的度数,进而得到∠BOF的度数,利用弧长公式求出弧BF长,即为圆锥的底面周长,求出圆锥底面半径即可;
(2)阴影部分面积=矩形AOED面积-三角形AOF面积-扇形EOF面积,求出即可.
(2)阴影部分面积=矩形AOED面积-三角形AOF面积-扇形EOF面积,求出即可.
解答: 解:(1)连接OE,
解:(1)连接OE,
∵CD与圆O相切,
∴OE⊥CD,且OE=OB=OF=BC=6cm,
∴矩形ABCD中,OA=AB-OB=9-6=3cm,
在Rt△AOF中,OA=3cm,OF=6cm,
∴cos∠AOF=
=
,即∠AOF=60°,AF=
=3
cm,
∴∠BOF=120°,
∴l弧长=
=4π,
则圆锥得地面半径为
=2cm;
(2)∵∠BOF=120°,∠EOB=90°,
∴∠EOF=30°,
∴S阴影=S矩形AOED-S△AOF-S扇形EOF=3×6-
×3×3
-
=18-
-3π.
 解:(1)连接OE,
解:(1)连接OE,∵CD与圆O相切,
∴OE⊥CD,且OE=OB=OF=BC=6cm,
∴矩形ABCD中,OA=AB-OB=9-6=3cm,
在Rt△AOF中,OA=3cm,OF=6cm,
∴cos∠AOF=
| 3 |
| 6 |
| 1 |
| 2 |
| OF2-OA2 |
| 3 |
∴∠BOF=120°,
∴l弧长=
| 120π×6 |
| 180 |
则圆锥得地面半径为
| 4π |
| 2π |
(2)∵∠BOF=120°,∠EOB=90°,
∴∠EOF=30°,
∴S阴影=S矩形AOED-S△AOF-S扇形EOF=3×6-
| 1 |
| 2 |
| 3 |
| 30π×62 |
| 360 |
9
| ||
| 2 |
点评:此题考查了切线的性质,扇形面积公式,弧长公式,勾股定理,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
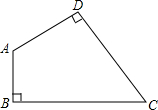 如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2
如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2