题目内容
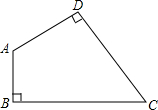 如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2
如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2| 3 |
考点:解直角三角形
专题:几何图形问题
分析:要想求得四边形ABCD的面积,必须加以辅助线使四边形变成可以求得面积的图形,根据图形特点和已知条件,可以延长BA、CD相交于E,然后求出即可.
解答: 解:延长BA、CD相交于E,如图:
解:延长BA、CD相交于E,如图:
∠C=360°-90°-90°-135°=45°
则△BCE和△ADE都是等腰直角三角形.
S四边形ABCD=S△BCE-S△ADE
=
×2
×2
-
×2×2
=6-2
=4.
答:四边形ABCD的面积是4.
 解:延长BA、CD相交于E,如图:
解:延长BA、CD相交于E,如图:∠C=360°-90°-90°-135°=45°
则△BCE和△ADE都是等腰直角三角形.
S四边形ABCD=S△BCE-S△ADE
=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
=6-2
=4.
答:四边形ABCD的面积是4.
点评:考查了解直角三角形,分析已知条件配合图形特点,巧妙加以辅助线,寻求突破.

练习册系列答案
相关题目
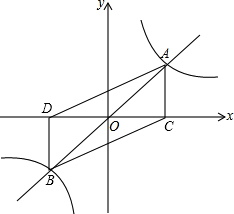 已知反比例函数
已知反比例函数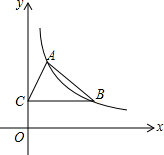 如图,函数y=
如图,函数y=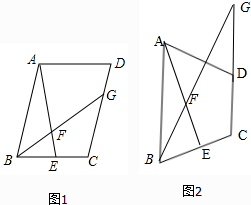 如图1,在?ABCD中,点E是BC边的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若
如图1,在?ABCD中,点E是BC边的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若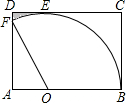 如图,在矩形纸片ABCD中,AB=9cm,BC=6cm,O在AB上,若以O为圆心,画弧与BC相切于B,与CD相切于点E,交AD于点F,连结FO,若把扇形BOF剪下,围成一个圆锥的侧面(不计接口尺寸).求:
如图,在矩形纸片ABCD中,AB=9cm,BC=6cm,O在AB上,若以O为圆心,画弧与BC相切于B,与CD相切于点E,交AD于点F,连结FO,若把扇形BOF剪下,围成一个圆锥的侧面(不计接口尺寸).求: