题目内容
2.阅读理解并填空:(1)为了求代数式x2+2x+3的值,我们必须知道x的值,若x=1,则这个代数式的值为6;若x=2,则这个代数式的值为11,…,可见,这个代数式的值因x的取值不同而变化,尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)把一个多项式进行部分因式分解可以来解决代数式值的最大(或最小)值问题,例如:x2+2x+3的最小值是2,这时相应的x的平方是1.
尝试探究并解答:
(3)求代数式x2-10x+35的最小值,并写出相应x的值.
(4)求代数式-x2-8x+15的最大值,并写出相应的x的值.
(5)改成已知y=-x2+6x-3,且x的值在数1-4(包含1和4)之间变化,试探求此时y的不同变化范围.(直接写出当x在哪个范围变化时,对应y的变化范围).
分析 (1)把x=1和x=2分别代入代数式x2+2x+3中,再进行计算即可得出答案;
(2)根据非负数的性质即可得出答案;
(3)先把给出的式子化成完全平方的形式,再根据非负数的性质即可得出答案;
(4)根据完全平方公式把给出的式子进行整理,即可得出答案;
(5)先把代数式化成完全平方的形式,再根据非负数的性质以及x的取值范围即可得出答案.
解答 解:(1)把x=1代入x2+2x+3中,得:12+2+3=6;
若x=2,则这个代数式的值为22+2×2+3=11;
故答案为6;11;
(2)根据题意可得:
x2+2x+3=(x2+2x+1)+2=(x+1)2+2,
∵(x+1)2是非负数,
∴这个代数式x2+2x+3的最小值是2,相应的x的平方是1.
故答案为2;1;
(3)∵x2-10x+35=(x-5)2+10,
∴代数式x2-10x+35的最小值是10,相应的x的值是5;
(4)∵-x2-8x+15=-(x+4)2+31,
∴-x2-8x+15的最大值是31,相应的x的值是-4;
(5)∵y=-x2+6x-3,
∴y=-(x-3)2+6,
∵x的值在数1~4(包含1和4)之间变化,
∴这时y的变化范围是:2≤y≤6.
点评 此题考查了因式分解的应用,用到的知识点是完全平方公式,非负数的性质,解题的关键是把给出的式子化成完全平方的形式进行解答.

练习册系列答案
相关题目
 根据图形填空:点B在直线BC上,图中有线段3条;以点B为端点的射线有3条.
根据图形填空:点B在直线BC上,图中有线段3条;以点B为端点的射线有3条. 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.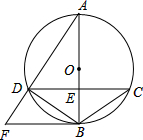 如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.若⊙O的半径为5,cos∠BCD=$\frac{4}{5}$,那么线段AD=8.
如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.若⊙O的半径为5,cos∠BCD=$\frac{4}{5}$,那么线段AD=8.