Question

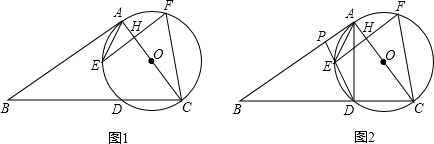
17．如图（1）△ABC以AC为直径作⊙O交边BC于点D，弦EF⊥AC于点H，连接AE、CF，若∠B+∠BAE=∠EFC．
（1）求证：∠ACB=2∠AEF；
（2）求证：DC=2OH；
（3）如图（2）连接AD，若AE平分∠BAD，tan∠B=$\frac{3}{4}$，OH=$\frac{9}{2}$，射线DE交AB于点P，求AP的长．

Answer 1

分析 （1）根据垂径定理得到$\widehat{AE}$=$\widehat{AF}$，EH=FH，根据等腰三角形的性质得到∠AEF=∠1，根据余角的性质得到∠1=∠2=∠AEF，即可得到结论；
（2）根据圆周角定理得到∠1=∠2=∠AEF，等量代换得到∠1=∠2=∠ACF，根据等腰三角形的性质得到OH=OM，推出OM是△ACD的中位线，根据三角形中位线的性质即可得到结论；
（3）根据等腰三角形的性质得到AC=CG，根据三角形外角的想知道的∠AGC=∠B+∠3，求得∠B=∠DAC，由于∠APE=∠APD，推出△PAE∽△PDA，根据三角形的性质得到$\frac{PA}{PD}=\frac{AE}{AD}=\frac{PE}{AP}=\frac{3\sqrt{5}}{12}=\frac{\sqrt{5}}{4}$，列方程即可得到结论．

解答 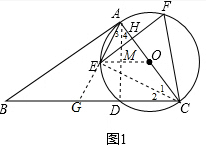解：（1）如图1，延长AE交BD于G，连CE，
∵EF⊥AC，
∴$\widehat{AE}$=$\widehat{AF}$，EH=FH，
∴∠AEF=∠1，CE=CF，∠F=∠HEC，
∵∠B+∠BAE=∠F，
∴∠AGC=∠F=∠HEC，
∵AC为⊙O的直径，
∴∠AEF=90°，
∴∠2+∠AEC=90°，
∵∠1+∠HEC=90°，
∴∠1=∠2=∠AEF，
∴∠ACB=2∠AEF；

（2）如图1，连接AD，OE交AD于M，
∵∠1=∠2=∠AEF，
∴∠1=∠2=∠ACF，
∴∠DCA=∠ECF，
∴AD=EF，
∴OH=OM，
∵O是AC的中点，OM⊥AD，CD⊥AD，
∴OM∥CD，
∴OM是△ACD的中位线，
∴OM=$\frac{1}{2}$CD，
∴OH=$\frac{1}{2}$CD，
∴CD=2OH；

（3）如图2，延长AE交BD于G，连CE，∠1=∠2，CE⊥AG，
∴AC=CG，∠AGC=∠GAC=∠4+∠DAC，
∵∠AGC=∠B+∠3，
∵∠3=∠4，
∴∠B=∠DAC，
∴OH=$\frac{9}{2}$，
∴OM=$\frac{9}{2}$，DC=9，
∵tanB=tan∠DAC=$\frac{3}{4}$，
∴AD=12，AC=15=CG，
∴DG=15-9=6，
∴AG=6$\sqrt{5}$，
∴AE=3$\sqrt{5}$=DE，
∵∠3=∠4=∠1=∠5，∠APE=∠APD，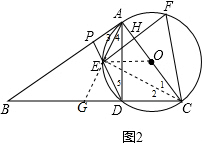
∴△PAE∽△PDA，
∴$\frac{PA}{PD}=\frac{AE}{AD}=\frac{PE}{AP}=\frac{3\sqrt{5}}{12}=\frac{\sqrt{5}}{4}$，
设PA=$\sqrt{5}$x，PD=4x，
∵PA²=PE•PD，
∴（$\sqrt{5}$x）²=（4x-3$\sqrt{5}$）•4x，
解得：x₁=0，x₂=$\frac{12\sqrt{5}}{11}$，
∴PA=$\frac{12\sqrt{5}}{11}$×$\sqrt{5}$=$\frac{60}{11}$．

点评 本题考查了圆周角定理，三角形的中位线的性质，相似三角形的判定和性质，勾股定理，证得△PAE∽△PDA是解决（3）小题的关键．