题目内容
 如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=
如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=| 3 |
| x |
| A、逐渐增大 | B、逐渐减小 |
| C、不变 | D、先增大后减小 |
考点:反比例函数系数k的几何意义
专题:
分析:因为△OAB的OA长度已经确定,所以只要知道点B到OA边的距离d就可知道△OAB 的面积变化情况【△OAB 的面积=
0A•d】,而点B到OA边的距离d即为点B的纵坐标,由点B是双曲线y=
(x>0)上的一个动点,在(x>0)第一象限y随x的增大y值越来越小,即d值越来越小,故△OAB 的面积减小.
| 1 |
| 2 |
| 3 |
| x |
解答:
解:设B(x,y).
∴S△OAB=
0A•y;
∵OA是定值,点B是双曲线y=
(x>0)上的一个动点,双曲线y=
(x>0)在第一象限内是减函数,
∴当点B的横坐标x逐渐增大时,点B的纵坐标y逐渐减小,
∴S△OAB=
0A•y会随着x的增大而逐渐减小.
故选:B.
∴S△OAB=
| 1 |
| 2 |
∵OA是定值,点B是双曲线y=
| 3 |
| x |
| 3 |
| x |
∴当点B的横坐标x逐渐增大时,点B的纵坐标y逐渐减小,
∴S△OAB=
| 1 |
| 2 |
故选:B.
点评:本题考查了反比例函数的性质:对于反比例函数y=
,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.
| k |
| x |

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
下列说法中不正确的是( )
| A、最小的正整数是1 |
| B、最大的负整数是-1 |
| C、有理数分为正数和负数 |
| D、绝对值最小的有理数是0 |
下列说法中,正确的有( )
①两个成轴对称的图形的对应点连线被对称轴垂直平分;②两个图形关于某直线对称,对应线段相等,对应角也相等;③有三条对称轴的三角形是等边三角形.
①两个成轴对称的图形的对应点连线被对称轴垂直平分;②两个图形关于某直线对称,对应线段相等,对应角也相等;③有三条对称轴的三角形是等边三角形.
| A、0个 | B、1个 | C、2个 | D、3个 |
 一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )
一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,Rt△ABC中,∠ABC=90°以AB为直径的⊙O交AB于点D,点E为BC的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°以AB为直径的⊙O交AB于点D,点E为BC的中点,连接DE.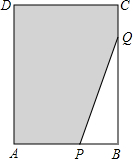 如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2.
如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2. 某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示: