题目内容
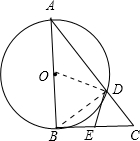
 如图,Rt△ABC中,∠ABC=90°以AB为直径的⊙O交AB于点D,点E为BC的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°以AB为直径的⊙O交AB于点D,点E为BC的中点,连接DE.(1)求证:DE是⊙O的切线.
(2)若∠BAC=30°,DE=3,求AD的长.
考点:切线的判定
专题:
分析:(1)如图,作辅助线;根据题意结合图形,证明∠ODE=90°,即可解决问题.
(2)首先求出BC=6,进而求出BD的值;运用直角三角形的性质求出AD的值,即可解决问题.
(2)首先求出BC=6,进而求出BD的值;运用直角三角形的性质求出AD的值,即可解决问题.
解答:
 (1)证明:连接OD、BD,
(1)证明:连接OD、BD,
∵AB为⊙O的直径,
∴∠ADB=∠CDB=90°;
又∵点E为BC的中点,
∴BE=DE,
∴∠BDE=∠EBD;
∵OA=OD,
∴∠OAD=∠ODA;
又∵∠OAD+∠OBD=90°,∠EBD+∠OBD=90°,
∴∠OAD=∠EBD,即∠ODA=∠BDE;
∴∠ODE=∠BDE+∠ODB=∠ODA+∠ODB=90°,
又∵点D在⊙O上,
∴DE是圆⊙O的切线.
(2)解:由(1)知BC=2DE=6,
又∵∠CBD=∠BAC=30°,
∴CD=3,BD=3
∴AB=6
;
由勾股定理得:AD=9.
 (1)证明:连接OD、BD,
(1)证明:连接OD、BD,∵AB为⊙O的直径,
∴∠ADB=∠CDB=90°;
又∵点E为BC的中点,
∴BE=DE,
∴∠BDE=∠EBD;
∵OA=OD,
∴∠OAD=∠ODA;
又∵∠OAD+∠OBD=90°,∠EBD+∠OBD=90°,
∴∠OAD=∠EBD,即∠ODA=∠BDE;
∴∠ODE=∠BDE+∠ODB=∠ODA+∠ODB=90°,
又∵点D在⊙O上,
∴DE是圆⊙O的切线.
(2)解:由(1)知BC=2DE=6,
又∵∠CBD=∠BAC=30°,
∴CD=3,BD=3
| 3 |
∴AB=6
| 3 |
由勾股定理得:AD=9.
点评:该题主要考查了切线的判定、圆周角定理及其推论、勾股定理、直角三角形的性质等几何知识点及其应用问题;牢固掌握圆周角定理及其推论、勾股定理等知识点是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
二次函数y=-(x+2)2-1的顶点坐标为( )
| A、(2,-1) |
| B、(2,1) |
| C、(-2,1) |
| D、(-2,-1) |
 如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=
如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=| 3 |
| x |
| A、逐渐增大 | B、逐渐减小 |
| C、不变 | D、先增大后减小 |

