Question

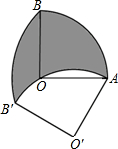如图，在扇形OAB中，∠AOB=90°，OA=3，将扇形OAB绕点A逆时针旋转n°（0＜n＜180）后得到扇形O′AB′，当点O在弧AB′上时，n为

 

，图中阴影部分的面积为

 

．

Answer 1

考点：扇形面积的计算,旋转的性质

专题：

分析：连接OO′，可知△OO′A为等边三角形，可求得n，连接AB′、AB，可知弓形AB和弓形AB′的面积相等，所以可知阴影部分的面积等于扇形BAB′的面积，计算扇形BAB′的面积可求得答案．

解答：解：连接OO′，
由旋转的性质可知OA=O′A，又OO′=O′A，
∴△OO′A为等边三角形，
∴n=60，
连接AB′、AB，可知∠BAB′=60°，S_弓形AOB=S_弓形AOB′，且AB=3

2

，
∴S_阴影=S_扇形BAB′=

60π×(3 2 )2

360

=3π．
故答案为：60；3π．

点评：本题主要考查旋转的性质及扇形的面积，由旋转得到S_弓形AOB=S_弓形AOB′是解题的关键．