题目内容
 如图,在△ABC中,∠A=60°,∠B=35°,点D、E分别在BC、AC的延长线上,则∠1=
如图,在△ABC中,∠A=60°,∠B=35°,点D、E分别在BC、AC的延长线上,则∠1=考点:三角形内角和定理,对顶角、邻补角
专题:
分析:根据三角形内角和定理求出∠ACB,根据对顶角相等求出即可.
解答:解:如图:

∵∠A+∠B+∠ACB=180°,∠A=60°,∠B=35°,
∴∠ACB=85°,
∴∠1=∠ACB=85°,
故答案为:85°.

∵∠A+∠B+∠ACB=180°,∠A=60°,∠B=35°,
∴∠ACB=85°,
∴∠1=∠ACB=85°,
故答案为:85°.
点评:本题考查了对顶角,三角形内角和定理的应用,解此题的关键是能关键三角形内角和定理求出∠ACB的度数,注意:三角形的内角和等于180°.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知⊙O的直径为13cm,如果直线和圆心的距离为7.5cm,那么直线和圆的公共点的个数为( )
| A、1 | B、3 | C、2 | D、0 |
以下列各组数为边长,能构成直角三角形的是( )
| A、5,7,8 | ||||
| B、1,2,3 | ||||
C、
| ||||
D、
|
 在△ABC中,AB=AC=10,BD是AC边上的高,DC=2,则BD等于( )
在△ABC中,AB=AC=10,BD是AC边上的高,DC=2,则BD等于( )A、2
| ||
| B、4 | ||
| C、6 | ||
| D、8 |
下列长度的三条线段中,能组成三角形的是( )
| A、3,4,8 |
| B、5,6,11 |
| C、4,6,7 |
| D、4,4,10 |
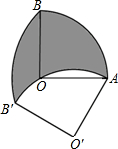 如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB′上时,n为
如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB′上时,n为 作图:在数轴上找到表示实数-
作图:在数轴上找到表示实数-