题目内容
 如图,AB切⊙O于点B,OA=2
如图,AB切⊙O于点B,OA=2| 3 |
 |
| BC |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
考点:弧长的计算
专题:计算题
分析:先根据切线的性质得∠ABO=90°,在Rt△ABO中,根据互余得到∠AOB=60°,根据含30度的直角三角形三边的关系OB=
OA=
,由于BC∥OA,所以∠OBC=∠AOB=60°,则可判断△OBC为等边三角形,得到∠BOC=60°,然后根据弧长公式计算劣弧
的弧长.
| 1 |
| 2 |
| 3 |
 |
| BC |
解答:解: 连结OB、OC,如图,
连结OB、OC,如图,
∵AB切⊙O于点B,
∴OB⊥AB,
∴∠ABO=90°,
在Rt△ABO中,∵∠A=30°,
∴∠AOB=60°,OB=
OA=
×2
=
,
∵BC∥OA,
∴∠OBC=∠AOB=60°,
而OB=OC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∴劣弧
的弧长=
=
.
故选A.
 连结OB、OC,如图,
连结OB、OC,如图,∵AB切⊙O于点B,
∴OB⊥AB,
∴∠ABO=90°,
在Rt△ABO中,∵∠A=30°,
∴∠AOB=60°,OB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵BC∥OA,
∴∠OBC=∠AOB=60°,
而OB=OC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∴劣弧
 |
| BC |
60•π•
| ||
| 180 |
| ||
| 3 |
故选A.
点评:本题考查了弧长的计算:弧长公式l=
(弧长为l,圆心角度数为n,圆的半径为R).也考查了切线的性质和含30度的直角三角形三边的关系.
| nπR |
| 180 |

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
某县为发展教育事业,加强了对教育经费的投入,2012年投入3000万元,预计2014年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
| A、3000x2=5000 |
| B、3000(1+x)2=5000 |
| C、3000(1+x%)2=5000 |
| D、3000(1+x)+3000(1+x)2=5000 |
九(1)班同学毕业的时候,每人都必须与其他任何一位同学合照一张双人照,全班共照相片780张,则九(1)班的人数是( )
| A、39 | B、40 | C、50 | D、60 |
为了完成下列任务,计划采用的调查方式合适的是( )
| A、了解我省中学生每天体育锻炼的时间,采用抽样调查的方式 |
| B、了解一沓钞票中有没有假钞,采用抽样调查的方式 |
| C、了解某种灯泡的使用寿命,采用普查的方式 |
| D、了解我国初中生每周阅读的时间,采用普查的方式 |
掷一枚均匀的骰子,前5次朝上的点数恰好是1~5,则第6次朝上的点数( )
| A、一定是6 |
| B、是6的可能性大于是1~5中的任意一个数的可能性 |
| C、一定不是6 |
| D、是6的可能性等于是1~5中的任意一个数的可能性 |
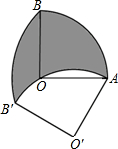 如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB′上时,n为
如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB′上时,n为 作图:在数轴上找到表示实数-
作图:在数轴上找到表示实数-